2021-09-28

Salesforce 開発者の JavaScript スキル(1)

JavaScript の基本概念について

trailhead.salesforce.com

JavaScript の概要、使用する理由、使用法
- 概要だけざっくり
  - もともとJSはHTMLを軽く動かすオプション的扱いだった
  - そのうち動的ページができてきた。サーバ(Salesforce)で処理する VF がそれ。
  - そのうち JS が ECMA 準拠で高機能になって、画面側で色々処理したり画面作れるようになった
  - これが LWC
JavaScript ランタイム テストに出る
- イベントやAPIの応答などがあると、そいつはキューに一旦確保される
- JS 実行ランタイムは、キューから一つづつそれを拾って、スタックメモリで実行を行う
JavaScript という言語個人的には Apex より馴染みがあって好きな言語です。
- 絶えず変化してる。ウン、毎年のように更新されてて、最新は ES2021／ES2022を知ろう | フューチャー技術ブログかな。
  ブラウザはガンガン追従してるよ！
- API は普遍的に採用されているわけではない
  ブラウザの実装状態によって動かなかったりするね！個人的に一番ひどいのは iOS の Safari がバグ多くでう〇こですね！
絶対に知っておくべきこと
- 大文字と小文字を区別する
  当たり前だ！というのは他言語ガンガンやってる人。「え？」と思うのは Apex 開発者。
  Apex は大文字小文字は関係ない
- var, let, const キーワードは必須。
  let, const はレキシカルスコープ(他言語と大体同じスコープ+変数寿命)だけど、var は Functionスコープって言って関数の実行単位のスコープを持つっていう分かりにくいヤツ。
  JavaScriptのスコープ総まとめ | 第1回スコープの種類とその基本 | CodeGrid この辺がおすすめ。
- 暗黙的な型の強制変換 テストに出る
  普通に parseInt とか使いましょう。
  let num1 = 9 * "3"; // 27 とかいう PHP 臭い挙動
  let num2 = 9 + "3"; // 93 でなぜか文字列結合ｗｗｗｗ
- Boolean 判定がかなりファジー
  false == ""; // true とか普通に行ける。
  型まで完全に比較するなら false === ""; // false とか使うべき。
  因みに !== とかもある
- false とみなされる値集
  - false
  - 0
  - "" や '' (空文字)
  - null
  - undefined (初期化してない変数や、存在しない変数名を指定したときの値)
  - NaN (算術エラー: 0 で割ったとか)
- this の意味が違う
  - class メソッド内の this は大体他の言語と意味合いは同じだけど、例えば <button onclick="hoge"> の時の function hoge() { console.log(this); } の this は button タグだったりするって話。
    JavaScript の this を理解する多分一番分かりやすい説明 - Qiita 多分これが一番わかりやすい
- 関数は値
  関数型言語やってる人御用達。「関数が第一級オブジェクト」という小難しい言い方できる。
  要するに、return に関数を返すことも、引数にすることもできる（高階関数という）。

2021-09-27

LSTM の概要

時系列データを利用するDeepLearningの一種。

LSTM = Long short-term memory
以前やってた RNN の一種だけど、記憶のやり方が異なる。

RNN はこれね…

white-azalea.hatenablog.jp

LSTM は以下のようなセルとゲートがあり、それぞれのゲートに学習パラメータを持ってる。

f:id:white-azalea:20210927224336p:plain

記憶セル : 過去の記憶を保持する
忘却ゲート : 過去の記憶を消す割合を調整する
入力ゲート : 新しい記憶を追加する割合を調整する
出力ゲート : 記憶セルの内容を出力に反する割合を調整する

加えて記憶セル → 積の間の Tanh も学習パラメータがあるので、学習パラメータが計4か所もあるという…

忘却ゲート

忘却ゲートはこんな感じ

$A^{(t)}_0 = \sigma ( X^{(t)} W_0 + Y^{(t-1)} V_0 + B_0 )$

$A^{(t)}_0$ は活性関数後の値。
$\sigma$ はシグモイド関数。
$X^{(t)}$ は現時点の入力。
$Y^{(t-1)}$ は前回の結果出力。

W,Bは重みとバイアス。これは前回までもそうだったので今更である。
入力ゲートと新しい記憶データの $Tanh$ はこんな感じになる

入力ゲート

$A^{(t)}_1 = \sigma ( X^{(t)} W_1 + Y^{(t-1)} V_1 + B_1 )$

まぁ内容は見たままやね。

新しい記憶データは

$A^{(t)}_2 = tanh ( X^{(t)} W_2 + Y^{(t-1)} V_2 + B_2 )$

こいつらって結構見たままなのよね

出力ゲート

$A^{(t)}_3 = \sigma ( X^{(t)} W_3 + Y^{(t-1)} V_3 + B_3 )$

というか活性関数通す連中だから基本楽ですよね。

しかしこれを微分するのか…気が滅入るな…

2021-09-15

確率周りの勉強続き

大数の法則

完全に一様分布を持つデータは回数を重ねるほど平均値は期待値に近づく

import numpy as np
import matplotlib.pyplot as plt

times = 1000
sample_array = np.array([1, 2, 3, 4, 5, 6])
number_cnt = np.arange(1, times + 1)  # 1, 2, 3, ... 1000

for i in range(5):
    # ランダムで 1000 回サイコロを振った累積値 3, 1, 5... とサイコロの目が出るなら 3, 4, 9... というリストになる
    p = np.random.choice(sample_array, times).cumsum()
    # 試行回数で各値を割って表示する
    plt.plot(p / number_cnt)
    plt.grid(True)

f:id:white-azalea:20210915224558p:plain

中心極限定理

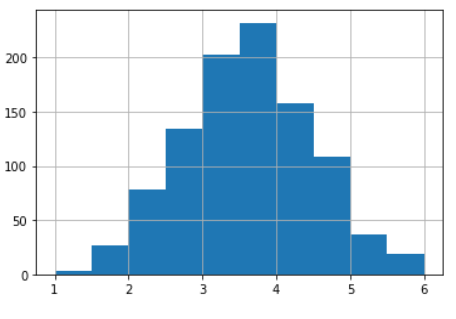
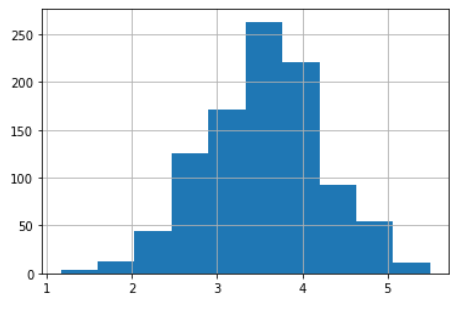
サイコロ等を投げる回数 N が増えれば増えるほどに標本平均が正規分布となっていく法則

def func_central(N):
    mean_array = np.array([])
    for i in range(1000):
        # ランダムで N 回サイコロを振った累積値リスト
        cum_var = np.random.choice(sample_array, N).cumsum() * 1.0
        # 累積値の最終値 / サイコロを振った回数 を平均に突っ込む
        mean_array = np.append(mean_array, cum_var[N-1] / N)
    # 平均値の出現回数をヒストグラムで表示
    plt.hist(mean_array)
    plt.grid(True)

func_central(4)

f:id:white-azalea:20210915224712p:plain f:id:white-azalea:20210915224816p:plain

2021-09-02

ダメ人間製造セット

日記

ただの紹介エントリ。
個人的に最悪なダメ人間製造セット

THANKO スマホタブレット対応超軽量折りたたみ式「仰向けゴロ寝デスク2」 TKGORODK

THANKO

Amazon

エレコムマウスワイヤレス (レシーバー付属) トラックボールハンディタイプ Relacon メディアコントロールボタン搭載静音ブラック M-RT1DRBK

エレコム

Amazon

仰向けごろ寝デスク＋片手操作可能な無線トラックボールマウス。
お勧めは Bluetooth 版。

仰向けごろ寝デスク２はノートパソコンやタブレットを固定したままごろ寝するためのツール。

f:id:white-azalea:20210902183732p:plain

ここに無線のトラックボールマウスということは寝っ転がったまま手すら延ばさずPCを操作できるという事。
どうですかね？ｗｗｗ

2021-08-31

iDeCo と NISA の目的の違い

iDeCo と NISA は設立目的が違う

まず管轄が違います。 NISA は金融庁、iDeCo は厚生労働省です。
またその設立の目的も異なります。

iDeCo はあくまで老後資金用

年金問題ですが、少子高齢化で、年金が下がるのが目に見えている。
「老後 2000万不足する」と政府が言い出してるのがいい例です。

誤解してはいけないのは、年金制度でもらえなくなるとか制度が終わるということは、日本国民が存在して労働人口がいる限りまずありません。
しかし老後の貧困を避けるだけの潤沢な資金を政府は用意することができません。

年金機構の資産運用はもう無理ぽ！ → 税優遇するから自分で年金作って☆
という丸投げから生まれた制度です。

iDeCo の節税効果

iDeCo は積み立て時は控除が受けれます。
リーマンで月2.5 万積み立てなら、年間 30 万、これが非課税対象になります。
仮に所得が年収 500 万なら、課税対象が 470 万に落ちます。
住民税、所得税合わせて 20% とした場合、100 万→94万 = 6 万節税になります。

iDeCo（イデコ）の節税効果・メリット | みずほ銀行

代わりに、受け取り時に税金がかかるほか、毎月運用費（現在最安値 171 円/月）がかかります。
まぁ投資運用しないなんて早々ないので、手数料は無視できるでしょう。

iDeCo・確定拠出年金はどの様に受取るのが良い？受取り方による税額計算の違い | りそな銀行確定拠出年金

尚、加入年齢に制限があります。

NISA は国の経済を守りたい

新しいＮＩＳＡ制度の概要と改正の狙い

これは、NISA制度の政策目的である成長資金の供給拡大を促しつつ、家計の安定的な資産形成をさらに推し進めていくことが目的である。

確かに皆タンス貯金で死蔵しがちだからね日本人…。
これを引き出して経済成長につなげたい…分かります。…がｗ

景気が上がってきたけど投資家は殆どが外国人…このままでは日本の株の殆どが海外に渡ってしまって、経済的に安全とは言えない。
なので、国内で株をなるべく保有させたい。という意図が透けて見えますね…。

当初年間 100 万、非課税期間 5 年で制度を作ったのですが、結局そこに手を付けたのは元々株の売買してた一部の人たちが乗り換えただけでした。
彼らは売って買ってを高速で繰り返してしまいます。これでは成長資金を維持させたいという目的は達成できません。
要するに成長株を長期保有してほしいという意図が達成されませんでした。

で、試行錯誤が始まりました。

100万なんて積み立てしにくい？じゃぁ月10万の 120万ならどうだ？
→ 年間 120万に → でもまだ増えない（泣

そこで、長期保有してもらうために「積み立てNISA(年間 40 万、20年無課税)」が作成されました。

NISAの節税効果

控除の類はありません☆
ただし、年間 120 万まで投資可能で、5 年以内なら投資で儲かった分は非課税です。

仮に、投資信託で月 2% 損益があるとして、10 万を突っ込んで 5 年放置すると 32 万…これを 5 で割ると 6.4 万。
これが非課税で、毎月 10 万突っ込んでると更にエグイ数字に…

これを売った時も非課税なので、まぁいいお金になりますね。

NISA は加入年齢は 18 以上で上限はありません。
つまり、生涯運用可能です。

2021-08-29

投資信託記録アプリのアップデート

white-azalea.hatenablog.jp

コレの続き。

github.com

アプリをアップデート。

口数の追加（よく見るこの数字）
最新の合計資産価値を更新したとき、各購入記録の「資産価値」を更新するロジックを、「口数」ベースで割り振るよう修正。

自分は積み立て NISA じゃなくて普通の NISA なんで、原則的に売ること前提の機能だね。

2021-08-26

三次元グラフを書いてみるテスト

Python3 学習勉強

ちょっとやってみた感じです。

import numpy as np

x,y = np.mgrid[10:100:2, 10:100:2]
pos = np.empty(x.shape + (2,))

pos[:, :, 0] = x
pos[:, :, 1] = y

np.mgrid[10:100:2, 10:100:2] で x, y にグリッドなデータを生成させます。
この形状は、 10 起点で 100 未満まで 2 ステップで生成します。（データ数は 1 軸 45 個）

x.shape は (45, 45) で、x, y はそれぞれこんな形状になります。

 array([[10, 10, 10, ..., 10, 10, 10],
       [12, 12, 12, ..., 12, 12, 12],
       [14, 14, 14, ..., 14, 14, 14],
       ...,
       [94, 94, 94, ..., 94, 94, 94],
       [96, 96, 96, ..., 96, 96, 96],
       [98, 98, 98, ..., 98, 98, 98]])

array([[10, 12, 14, ..., 94, 96, 98],
       [10, 12, 14, ..., 94, 96, 98],
       [10, 12, 14, ..., 94, 96, 98],
       ...,
       [10, 12, 14, ..., 94, 96, 98],
       [10, 12, 14, ..., 94, 96, 98],
       [10, 12, 14, ..., 94, 96, 98]])

作成した pos はこの時点で

(45, 45, 2)
array([[[10., 10.],
        [10., 12.],
        [10., 14.],
        ...,
        [10., 94.],
        [10., 96.],
        [10., 98.]],

       [[12., 10.],
        [12., 12.],
        [12., 14.],
        ...,
        [12., 94.],
        [12., 96.],
        [12., 98.]],

       [[14., 10.],
        [14., 12.],
        [14., 14.],
        ...,
        [14., 94.],
        [14., 96.],
        [14., 98.]],

       ...,
show more (open the raw output data in a text editor) ...

        [98., 12.],
        [98., 14.],
        ...,
        [98., 94.],
        [98., 96.],
        [98., 98.]]])

まさに座標ですね。
ここにデータを肉付けします

from scipy.stats import multivariate_normal

rv = multivariate_normal([50, 50], [[100, 0], [0, 100]])
z = rv.pdf(pos)

multivariate_normal の引数を見ていくと、z,y ともに平均値 50、[[100, 0], [0, 100]] は分散共分散行列(後述に詳細。分散100, 共分散0)
この時の z はこんな感じになっている。

(45, 45)
array([[1.79105293e-10, 3.90713230e-10, 8.18909735e-10, ...,
        3.33805656e-11, 1.35715252e-11, 5.30141552e-12],
       [3.90713230e-10, 8.52330075e-10, 1.78642887e-09, ...,
        7.28187781e-11, 2.96059059e-11, 1.15648909e-11],
       [8.18909735e-10, 1.78642887e-09, 3.74423972e-09, ...,
        1.52623463e-10, 6.20520695e-11, 2.42392656e-11],
       ...,
       [3.33805656e-11, 7.28187781e-11, 1.52623463e-10, ...,
        6.22126874e-12, 2.52937912e-12, 9.88045888e-13],
       [1.35715252e-11, 2.96059059e-11, 6.20520695e-11, ...,
        2.52937912e-12, 1.02836881e-12, 4.01709481e-13],
       [5.30141552e-12, 1.15648909e-11, 2.42392656e-11, ...,
        9.88045888e-13, 4.01709481e-13, 1.56918905e-13]])

それぞれの位置に一つづつ値が入っている形かな。
これを作画すると

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure(dpi=100)
ax = Axes3D(fig)

ax.plot_wireframe(x, y, z)

ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x, y)')

ax.ticklabel_format(style='sci', axis='z', scilimits=(0, 0))

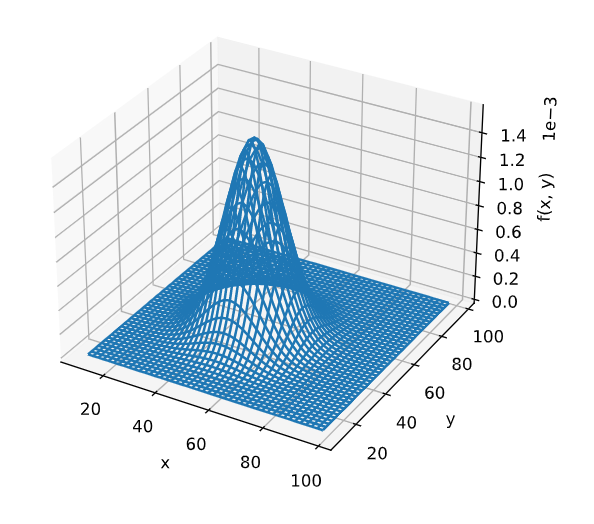
f:id:white-azalea:20210826215900p:plain