ニューロンと過学習の割合を観察する

検証内容

アルゴリズムと過学習の関係をざっくり記載する。
設定は以下の感じ

img_size   = 8
n_mid      = 32
n_out      = 10
eta        = 0.001
epochs     = 301
batch_size = 32
interval   = 10

因みにCNNの特徴抽出はせず、あくまでニューロンでの判定のみで行う。

中間層ニューロンを 32 個、バッチサイズ 32 で、エポック 301 回。
単純にニューロン食わして処理するとこんな感じ。

時間経過で誤差が広がる（過学習）が起きてるというよりは、単純にこのアルゴリズムでは精度が上がらないという事かもしれない。
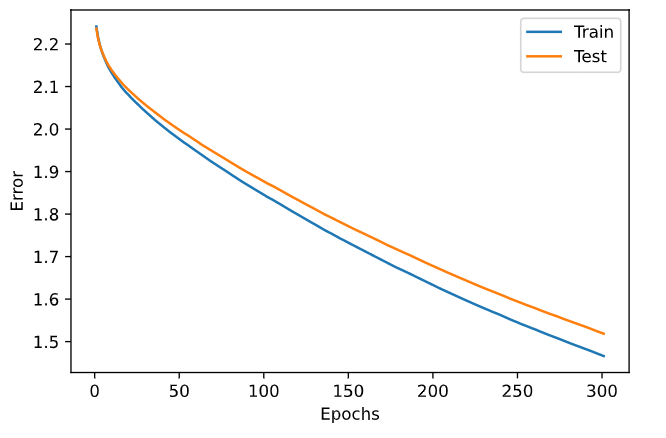
AdaGrad アルゴリズムを適用するとこんな感じ

学習係数に圧がかかってくるので、学習自体が遅くなる。
それによって学習が収束するのがかなり遅くなり、300 回程度では良い結果にならなかった。
ドロップ層を追加したのかこんな感じ

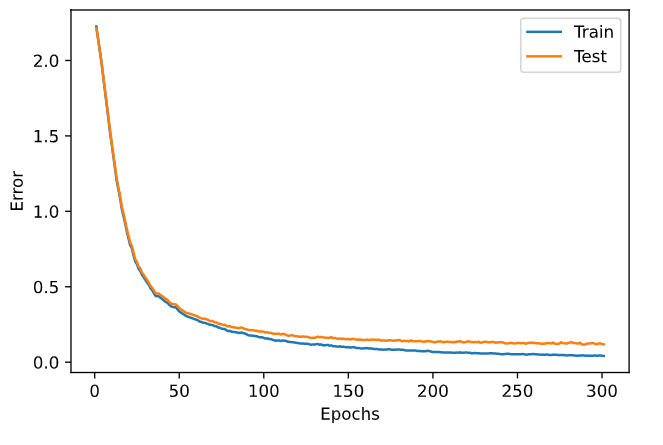
ニューロンの学習が確立的になるので、学習が微妙にガクガクする。
AdaGrad を使うべきかどうかは状況によるのかもしれない。

両方適用するなら、学習回数を更に増やす必要がありそう。

検証ソース

import numpy as np
import matplotlib.pyplot as plt

# System settings
img_size   = 8
n_mid      = 32
n_out      = 10
eta        = 0.001
epochs     = 301
batch_size = 32
interval   = 10

# Source data
from sklearn import datasets
from sklearn.model_selection import train_test_split
digits_data = datasets.load_digits()
# Data standardarise
input_data  = np.asarray(digits_data.data)
input_data  = (input_data - np.average(input_data)) / np.std(input_data)
# create correct data
correct = np.asarray(digits_data.target)
# to one-hot correct result
correct_data = np.zeros((len(correct), n_out))
for i in range(len(correct)):
    correct_data[i, correct[i]] = 1

# Split train and test datas.
X_train, X_test, t_train, t_test = train_test_split(input_data, correct_data)

def relu(u):
    return np.where(u <= 0, 0, u)

def differential_relu(u, y, t):
    return t * np.where(u <= 0, 0, 1)

def softmax(u):
    return np.exp(u)/np.sum(np.exp(u), axis=1, keepdims=True)

def differential_softmax(u, y, t):
    return y - t

class BaseLayer:
    def forward(self, x):
        return x
    def backward(self, grad_y):
        return grad_y
    def update(self, eta):
        pass

class Dropout(BaseLayer):
    def __init__(self, dropout_rate):
        self.dropout_rate = dropout_rate
    def forward(self, x, is_train=True):
        if is_train:
            rand = np.random.rand(*x.shape)
            self.dropout = np.where(rand > self.dropout_rate, 1, 0)
            self.y = x * self.dropout
        else:
            self.y = (1 - self.dropout_rate) * x
        return self.y
    def backward(self, grad_y):
        self.grad_x = grad_y * self.dropout
        return self.grad_x

class CommonLayer(BaseLayer):
    def __init__(self, n_upper, n, activation_func, differential_func):
        self.w = np.random.randn(n_upper, n) * np.sqrt(2 / n_upper)
        self.b = np.zeros(n)
        self.activation_func = activation_func
        self.differential_func = differential_func
    def forward(self, x):
        self.x = x
        self.u = np.dot(x, self.w) + self.b
        self.y = self.activation_func(self.u)
        return self.y
    def backward(self, grad_y):
        delta = self.differential_func(self.u, self.y, grad_y)
        self.grad_w = np.dot(self.x.T, delta)
        self.grad_b = np.sum(delta, axis=0)
        self.grad_x = np.dot(delta, self.w.T)
        return self.grad_x
    def update(self, eta):
        self.w -= eta * self.grad_w
        self.b -= eta * self.grad_b

class AdaLayer(CommonLayer):
    def __init__(self, n_upper, n, activation_func, differential_func):
        super().__init__(n_upper, n, activation_func, differential_func)
        self.h_w = np.zeros((n_upper, n)) + 1e-8
        self.h_b = np.zeros((n)) + 1e-8
    def update(self, eta):
        self.h_w += (self.grad_w * self.grad_w)
        self.h_b += (self.grad_b * self.grad_b)
        self.w -= eta / np.sqrt(self.h_w) * self.grad_w
        self.b -= eta / np.sqrt(self.h_b) * self.grad_b

class MiddleLayer(CommonLayer):
    def __init__(self, n_upper, n):
        super().__init__(n_upper, n, relu, differential_relu)

class OutputLayer(CommonLayer):
    def __init__(self, n_upper, n):
        super().__init__(n_upper, n, softmax, differential_softmax)

# Define layers and functions.
layers = [
    MiddleLayer(img_size*img_size, n_mid),
    MiddleLayer(n_mid, n_mid),
    #Dropout(0.5),
    #MiddleLayer(n_mid, n_mid),
    #Dropout(0.5),
    OutputLayer(n_mid, n_out)
]

def forward(x):
    for layer in layers:
        x = layer.forward(x)
    return x


def backward(t):
    grad_y = t
    for layer in reversed(layers):
        grad_y = layer.backward(grad_y)
    return grad_y


def update_grad():
    for layer in layers:
        layer.update(eta)

def calc_error(x, t):
    y = forward(x)
    return -np.sum(t * np.log(y + 1e-7)) / len(y)


def calc_accuracy(x, t):
    y = forward(x)
    count = np.sum(np.argmax(y, axis=1) == np.argmax(t, axis=1))
    return count / len(y)

# container for errors
error_record_train = []
error_record_test = []

n_batch = len(X_train)
for i in range(epochs):

    # random data gets.
    index_random = np.arange(len(X_train))
    np.random.shuffle(index_random)

    for j in range(n_batch):
        # get mini-batch
        mb_index = index_random[j*batch_size : (j+1)*batch_size]
        x_mb = X_train[mb_index, :]
        t_mb = t_train[mb_index, :]

        # forward and backword
        forward(x_mb)
        backward(t_mb)

        # parameter update
        update_grad()
    
    # get calc errors.
    error_train = calc_error(X_train, t_train)
    error_record_train.append(error_train)
    error_test = calc_error(X_test, t_test)
    error_record_test.append(error_test)

    # output error rate par inteval
    if i % interval == 0:
        print(f'Epoch: {i+1}/{epochs}, Error_train: {error_train}, Error_test: {error_test}')

plt.plot(range(1, len(error_record_train) + 1), error_record_train, label="Train")
plt.plot(range(1, len(error_record_test) + 1), error_record_test, label="Test")
plt.legend()

plt.xlabel("Epochs")
plt.ylabel("Error")
plt.show()

# calc accuracy
acc_train = calc_accuracy(X_train, t_train)
acc_test = calc_accuracy(X_test, t_test)

print(f"Acc_train: {acc_train * 100}%, Acc_test: {acc_test * 100}%")