技術をかじる猫

適当に気になった技術や言語、思ったこと考えた事など。

JavaScript でニューラルネットを実行

Javascript アルゴリズム 学習 日記

前回のニューラルネットの分類で、アヤメの判別を実装しました。

white-azalea.hatenablog.jp

この学習データを JavaScript に持って行って動かそうとしたのが今回。

学習データを取り出そう

ニューロンの学習した重みとバイアスを JSON 化して取り出すようメソッド追加し、

import json

class Neuron:
    # 中略
    
    def show(self):
        print(json.dumps(self.w.tolist()))
        print(json.dumps(self.b.tolist()))

学習完了後にその値を取得します。

middle.show()
output.show()

[[-0.1645569757531888, 0.705461787072002, 0.13634643058513146, -0.001427639477009482, -0.37761246456078673, 0.32594566195486246, -0.17540383608743443, -0.637910226879948], [1.2405711145126166, 2.619979392767813, -0.8480757978236683, -0.34862875404728705, 0.6081766688709285, 2.1609719770773466, 1.1812526170586088, -0.10568548347423115], [-4.74027409643627, -8.512471290631712, 3.0535213927424927, 0.6853620335528933, -3.021058907040047, -7.302407221156781, -4.505304631691936, -1.458038332845281], [-2.6381391656274893, -5.0742956034421365, 1.6448946680125553, 0.321396808734011, -1.629813019140954, -4.235682116890767, -2.519697996486675, -0.7485783120615989]]
[1.3354703014752847, 2.856479211057539, -0.36041020389500916, -0.09619435431305065, 0.5270124844477969, 2.3500865314253825, 1.225318793483202, -0.5722749346649912]
[[3.3900843132512795, 0.3336196951711783, -3.707400474181074], [6.873749691931951, 1.4723979662987134, -8.337604254104868], [-4.032894687445366, 0.20291576621871618, 3.82277459252311], [-1.4497941475896428, 0.3517295106421541, 1.1299533286177883], [1.920858740500269, 0.21229798170387007, -2.151150281026468], [5.754690191389036, 0.9299055788952119, -6.690439208956392], [3.1882961310528275, 0.2901387295306705, -3.4911286154994707], [0.47133299264734746, 0.3382463002700566, -0.8153830951792407]]
[-6.786999325197024, 0.8398018579145571, 5.919115463040789]

JavaScript に適用する

そして利用したものは math.js

techc.omorita.com mathjs.org

これを読み込んで適用したコードが以下です

続きを読む

自作ニューラルネット(分類型)を作って、色々やってみる

今度は分類問題に対応した NN 実装を考える。
とはいえ、テンプレは 前回記事 で作ってるので、さっくり定義する

import numpy as np
import matplotlib.pyplot as plt

%matplotlib inline

wb_width = 0.01 # 重みバイアスの広がり方
epoch    = 101  # 学習データ数
eta      = 0.1  # 学習係数

# 各層のニューロン数
n_in  = 2
n_mid = 6
n_out = 2

class Neuron:
    def __init__(self, n_upper, n, activation_function, differential_function):
        self.w = wb_width * np.random.randn(n_upper, n)
        self.b = wb_width * np.random.randn(n)
        self.grad_w = np.zeros((n_upper, n))
        self.grad_b = np.zeros((n))
        self.activation_function = activation_function
        self.differential_function = differential_function

    def update(self, eta):
        self.w -= eta * self.grad_w
        self.b -= eta * self.grad_b
    
    def forward(self, x):
        self.x = x
        u = x.dot(self.w) + self.b
        self.y = self.activation_function(u)
        return self.y

    def backword(self, t):
        delta = self.differential_function(self.y, t)
        self.grad_w = self.x.T.dot(delta)
        self.grad_b = np.sum(delta, axis=0)
        self.grad_x = delta.dot(self.w.T)
        return self.grad_x


class Output(Neuron):
    pass


class Middle(Neuron):
    def backword(self, grad_y):
        delta = self.differential_function(grad_y, self.y)
        self.grad_w = self.x.T.dot(delta)
        self.grad_b = delta.sum(axis = 0)
        self.grad_x = delta.dot(self.w.T)
        return self.grad_x

判定の場合、出力層が異なってくる

シグモイド関数はこんな式なので

f(x) = \frac{1}{1 + e^{-x}} \\ \delta_j = \partial y_j (1 - y_j)y_j 
def sigmoid(u):
    """シグモイド関数"""
    return 1 / (1 + np.exp(-u))


def differential_sigmod(grad_y, y):
    """シグモイド関数の勾配関数"""
    return grad_y * (1 - y) * y

出力層のソフトマックス関数 + 交差エントロピーは 過去計算 した式を拝借して

E(t,y) = - \sum_x t_x log(y_x) ... 交差エントロピー誤差 \\ y = \frac{exp(x)}{\sum^n_{k=1} exp(k)} .. ソフトマックス関数
E = - \sum_k t_k log( \frac{exp(u_k)}{ \sum_k exp(u_k) } ) \\ \delta_k = -t_k + y_k 
def soft_max(u):
    """ ソフトマックス関数 """
    return np.exp(u) / np.sum(np.exp(u), axis = 1, keepdims=True)


def differential_softmax(y, t):
    """ソフトマックス + 交差エントロピー の勾配関数"""
    return y - t
続きを読む

ニューラルネット実装

勉強 アルゴリズム Python3

今回やったこと：

  • 入力: 正弦波（ sign(x) ）を学習させて、-1 - 1 までの整数食わしたら sin を返す
  • 中間層: シグモイド関数(3 個)
  • 出力層: 恒等関数
  • 損失関数: 二乗和誤差
  • 最適化アルゴリズム: 勾配降下法
  • バッチサイズ: 1

で実装する。

まずは学習データその他

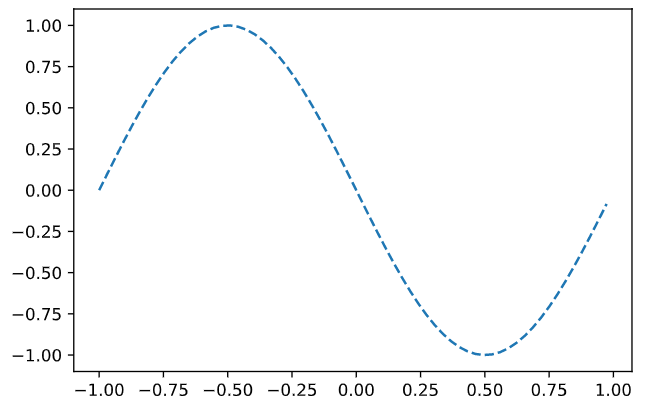
import numpy as np
import matplotlib.pyplot as plt

%matplotlib inline

wb_width = 0.01 # 重みバイアスの広がり方
epoch    = 2001 # 学習データ数
eta      = 0.1  # 学習係数

input_data   = np.arange(0, np.pi * 2, 0.1) # 学習データ
correct_data = np.sin(input_data)           # 正解データ
input_data   = (input_data - np.pi) / np.pi # -1 - 1 にデータを整形
n_data       = len(correct_data)            # データ数

# 各層のニューロン数
n_in  = 1
n_mid = 3
n_out = 1


# 学習データのプロット
plt.plot(input_data, correct_data)
plt.show()

f:id:white-azalea:20210308231807p:plain

出力層の勾配を考える。参考は 前回の記事 でやったやつ。
二乗和誤差と恒等関数の組み合わせだと、 \delta の値は

\delta_k = y_k - t_k

で、残りのパラメータは

\partial w_{jk} = y_j \delta_k (重み勾配) \\ \partial b_k = \delta_k (バイアス勾配) \\ \partial y_j = \sum^n_{r=1} \delta_r w_{jr} (一つ上の層の出力勾配) 
class Neuron:
    def __init__(self, n_upper, n, activation_function, differential_function):
        self.w = wb_width * np.random.randn(n_upper, n)
        self.b = wb_width * np.random.randn(n)
        self.grad_w = np.zeros((n_upper, n))
        self.grad_b = np.zeros((n))
        self.activation_function = activation_function
        self.differential_function = differential_function

    def update(self, eta):
        self.w -= eta * self.grad_w
        self.b -= eta * self.grad_b
    
    def forward(self, x):
        self.x = x
        u = x.dot(self.w) + self.b
        self.y = self.activation_function(u)
        return self.y

    def backword(self, t):
        delta = self.differential_function(self.y, t)
        self.grad_w = self.x.T.dot(delta)
        self.grad_b = np.sum(delta, axis=0)
        self.grad_x = delta.dot(self.w.T)
        return self.grad_x


def identity_func(u):
    """恒等関数"""
    return u


def differential_output(y, t):
    """恒等関数+二乗和誤差の微分"""
    return y - t


class Output(Neuron):
    pass

重みとバイアスは共通の作りなので、Neuron として独立。
forward で順伝播したときに、それぞれの値をクラス内変数に格納する。
backword で格納した値と、目標値 t を受け取って勾配を作る。

続きを読む

ニューラルネットワーク各階層の勾配計算式

学習 日記 アルゴリズム

勾配計算式

w を重み、 b をバイアス、 E を誤差(損失関数出力)とするとこんな形状で定式化されてる。
この辺はいくつかの書籍見て、ようやっと飲み込めた感じ…。

数式を飲み込むのにはそれなりに時間を要したけど…。

  • 出力層
\delta_k = \frac{\partial E}{\partial u_k} = \frac{\partial E}{\partial y_k} \frac{\partial y_k}{\partial u_k} \\ \partial w_{jk} = \frac{\partial E}{\partial w_{jk}} = y_j \delta_k (重み勾配) \\ \partial b_k = \frac{\partial E}{\partial b_k} = \delta_k (バイアス勾配) \\ \partial y_j = \frac{\partial E}{\partial y_j} = \sum^n_{r=1} \delta_r w_{jr} (一つ上の層の出力勾配)
  • 中間層
\delta_j = \frac{\partial E}{\partial u_j} = \partial y_j \frac{\partial y_k}{\partial u_j} \\ \partial w_{ij} = \frac{\partial E}{\partial w_{ij}} = y_i \delta_j (重み勾配) \\ \partial b_j = \frac{\partial E}{\partial b_j} = \delta_j (バイアス勾配) \\ \partial y_i = \frac{\partial E}{\partial y_i} = \sum^m_{q=1} \delta_q w_{iq} (一つ上の層の出力勾配)

結局のところ、 \delta_n さえ算出できれば、残りの計算式は芋づるで計算できることになる。

続きを読む

ニューラルネットの形状に関して

エポックとバッチ

1エポック = 全データを 1 回学習すること。
教師データのセット単位を 1 バッチ。

1 エポック = 複数バッチ

バッチ学習

バッチサイズ = エポックサイズ の学習のこと。
学習が安定してて高速ではあるが、局所解にハマりやすい。

オンライン学習

バッチサイズが 1 となる。
個々のデータに振り回されるので、バーストには弱いが、局所解にとらわれにくい。

ミニバッチ学習

訓練データを複数のバッチに分割して、バッチ単位で重みとバイアスの学習を行う。
局所解に囚われにくいし、個々のデータで振れ幅もさほどではない。

1000 の教師データがあるとき、

  • バッチ学習「1000で1回重みとバイアス計算を行う」
  • オンライン学習「1エポック当たり 1000 回学習するよ」
  • ミニバッチ学習「1バッチ 50で設定したら、20 回学習するよ」

行列での演算

バッチサイズを 8 入力数(入力層のニューロン数) 3 とすると、入力を表す行列サイズは 8x3。
バッチサイズが 1 の時、1x3 になるので、ベクトルの様な形状になる。

試しに 4x3 (バッチサイズ 2)の思考実験をすると

import numpy as np


X = np.array([
    [1, 2, 3, 4],
    [4, 5, 6, 7]
])

W = np.array([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9],
    [10, 11, 12]
])

X.dot(W)

array([[ 70,  80,  90],
       [136, 158, 180]])

もう少し汎用的に考えると バッチサイズ h 、入力層 m 、ニューロン数 n の行列はこんな感じか

XW = \left( \begin{array}{xxxx} x_{11} & x_{12} & ... & x_{1m} \\ x_{21} & x_{22} & ... & x_{2m} \\ ... & ... & ... & ... \\ x_{h1} & x_{h2} & ... & x_{hm} \end{array} \right) \left( \begin{array}{xxxx} w_{11} & w_{12} & ... & w_{1n} \\ w_{21} & w_{22} & ... & w_{2n} \\ ... & ... & ... & ... \\ w_{m1} & w_{m2} & ... & w_{mn} \end{array} \right)

うげ…でも数式書いてみると理解できる。
この時、座標 1,1 の結果は

x_{11}w_{11} + x_{12}w_{21} + ... + x_{1m}w_{m1} \\ = \sum^m_{k=1} x_{1k}w_{k1}

となるので、同様に考えて

XY = \left( \begin{array}{xxxx} \sum^m_{k=1} x_{1k}w_{k1} & \sum^m_{k=1} x_{1k}w_{k2} & ... & \sum^m_{k=1} x_{1k}w_{kn} \\ \sum^m_{k=1} x_{2k}w_{k1} & \sum^m_{k=1} x_{2k}w_{k2} & ... & \sum^m_{k=1} x_{2k}w_{kn} \\ ... & ... & ... & ... \\ \sum^m_{k=1} x_{hk}w_{k1} & \sum^m_{k=1} x_{hk}w_{k2} & ... & \sum^m_{k=1} x_{hk}w_{kn} \end{array} \right)

で、バイアスはニューロン毎に定義されるので数は ニューロン数と同数の n

XY+B = \left( \begin{array}{xxxx} \sum^m_{k=1} x_{1k}w_{k1} + b_1 & \sum^m_{k=1} x_{1k}w_{k2} + b_2 & ... & \sum^m_{k=1} x_{1k}w_{kn} + b_n \\ \sum^m_{k=1} x_{2k}w_{k1} + b_1 & \sum^m_{k=1} x_{2k}w_{k2} + b_2 & ... & \sum^m_{k=1} x_{2k}w_{kn} + b_n \\ ... & ... & ... & ... \\ \sum^m_{k=1} x_{hk}w_{k1} + b_1 & \sum^m_{k=1} x_{hk}w_{k2} + b_2 & ... & \sum^m_{k=1} x_{hk}w_{kn} + b_n \end{array} \right) = U

ここに活性関数 f(x) を適用すると結果 Y は Y = f(U)

コード的に関係性を書くと

## 値は適当だけど、実装的にはこな感じ

X = np.array([
    [1, 2, 3, 4],
    [4, 5, 6, 7]
])

W = np.array([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9],
    [10, 11, 12]
])

B = np.array([ 1, 2, 3 ])

U = X.dot(W) + B

print(U)

def sigmoid(u):
    return 1 / (1 + np.exp(-u))

sigmoid(U)

さて、ネタは揃った、いや、揃っちゃった（汗
後はこの値に最終層(恒等関数 or ソフトマックス関数)+誤差関数 を含んだ状態で微分して、勾配降下法で W, B の値を更新すればニューラルネットワークの学習ができるはず。

次回は微分地獄かー（汗

最適化アルゴリズム

と言っても機械学習的な意味で。

単純に勾配降下法を適用すると、局所解に捕まる問題は先に述べた通り。
分かりやすくサンプルを考えてみると

import numpy as np
import matplotlib.pyplot as plt


def func(x):
    return x*x*x*x + 2*x*x*x + -38*x*x + 2*x


X = np.arange(-10, 10, 0.02)
Y = func(X)

plt.plot(X, Y)
plt.show()

f:id:white-azalea:20210303203211p:plain

微分済みの関数は

def delta_func(x):
    return 4*x*x*x + 6*x*x -76*x + 2


# ここに 7,5 を突っ込むと
delta_func(7.5)  # 1457.0

傾斜凄いので、学習バイアスを仮に 0.001 位で想定すると

6.043
5.398451459972
5.002559811688421
4.729832392627848
4.529821496454675
4.377177480355534
4.257423546210319
4.161559438372887
4.08363734432107
4.019540738521101
3.9663154081729166
3.921778562920445
3.8842783889882955
3.8525397914062047
3.8255618877089477
中略
3.658931080932697
3.658743374723007
3.6585797983577586
3.658437247050682
3.658313016197765
3.658204749631204
3.6581103946042393
3.6581103946042393

とまぁこんな感じで、明らかに x=-5.... の方が正解にもかかわらず途中の 3.7 近辺に捕まってしまう。
この局所解を回避するのが最適化アルゴリズムと言ってるご様子。

確率的勾配降下法

訓練用データの中からパラメータの更新毎に、ランダムなサンプルを選び出すことで、局所解に捕まりにくくする。
要するに開始位置をランダムに指定するだけだ。

運よく 0 以下で始まれば最も値の小さい箇所に行ける。

Momentum

確率的勾配降下法に、慣性項を設けたというもの。
前回の更新量に追加でいくらかの値を設定する。

alpha = 0.001
beta = 2.7

current = 7.5
old = 0
last_w = 0

while abs(current - old) >= 0.0001:
    val = delta_func(current)
    old = current
    new_w = - val * alpha
    current = current + new_w + last_w * beta
    last_w = new_w
    print(current)

6.043
1.4645514599719993
-0.19185848304183395
0.01781967384422567
-0.028117364030085537
-0.034007546495780354
-0.049781152307481306
-0.06797555468750062
-0.0908220708732037
-0.11919109008260265
-0.15449030499302088
中略
-5.191354001667161
-5.180269368221342
-5.1771810299574925
-5.180181249424525
-5.184162051676043
-5.185922174066375
-5.185379292975573
-5.184060245776873
-5.183254760318419
-5.183254259207195

見ての通り、下がるときに慣性を利用して追加で下がるので、パラメータさえ合ってれば局所解を乗り越えていく。

AdaGrad

2011 年に現れたアルゴリズムで、学習が進むたびに学習係数を減らそうという試み。

h \leftarrow h + (\frac{\partial E}{\partial w})^2 \\ w \leftarrow w - \eta \frac{1}{\sqrt{h}}\frac{\partial E}{\partial w} 
import math

h = 0
current = 7.5
old = 0

while abs(current - old) >= 0.0001:
    val = delta_func(current)
    h = h + val * val
    new_w = - val / math.sqrt(h)
    old = current
    current = current + new_w
    print(current)

print(current)

見ればわかるが、ガンガン変化量を削られるｗ

6.5
5.991688924667466
5.646410961134836
5.386994732474357
5.181464168891868
5.013125259836374
4.87204852326966
4.7518067607144445
4.647984515962909
4.557410990822424
4.47772972020331
4.407140798818975
4.344238282940154
4.287903250227089
4.23723099543947
4.1914800066613
4.150035310462555
4.1123815712304745
4.078082977842838
4.04676795652729
4.018117381523742
3.991855364159257
3.9677419716725204
3.945567410183514
3.925147332371601
3.906319018896746
3.8889382456169352
3.8728766941891757
3.8580197969761705
3.8442649318798843
3.8315199012281496
3.8197016428478148
3.808735132162399
3.798552442405527
3.789091936457758
3.780297568841414
3.772118280375192
3.764507471142559
3.757422539948691
3.7508244804687685
3.744677525931404
3.738948835515955
3.733608216734055
3.728627878962639
3.723982214036123
3.719647600419263
3.7156022279933074
3.711825940915271
3.7083000963686423
3.705007437325738
3.7019319776970567
3.6990588984593322
3.6963744535380294
3.6938658843770793
3.6915213422630684
3.689329817586468
3.6872810753218084
3.6853655960944005
3.68357452227539
3.6818996086112543
3.680333176949806
3.6788680746735536
3.677497636493863
3.6762156492967013
3.6750163197634835
3.6738942445193583
3.672844382586653
3.6718620299436235
3.670942796008503
3.6700825818864313
3.6692775602324965
3.668524156598014
3.6678190321395934
3.6671590675816272
3.6665413483327454
3.665963150665686
3.665421928878012
3.664915303358293
3.66444104948883
3.6639970873218672
3.663581471971482
3.663192384668147
3.662828124427272
3.6624871002869765
3.662167824073909
3.661868903659179
3.6615890366694464
3.6613270046208934
3.6610816674463065
3.6608519583877244
3.660636879229203
3.6604354958461323
3.660246934049288
3.660070375703399
3.6599050551014836
3.6597502555775594
3.659605306341589
3.659469579521657
3.6593424873994564
3.6592234798261245
3.6591120418063894
3.6590076912398155
3.6589099768087188
3.6589099768087188

この h が毎回デカくなるから、学習もその都度抑えられるという仕組みだが、弱点として途中で h がデカくなりすぎて更新が止まることがある点。
今回は見事にそれ。

RMSProp

論文は存在してない？

h \leftarrow \rho h + (1 - \rho) (\frac{\partial E}{\partial w})^2 \\ w \leftarrow w - \eta \frac{1}{\sqrt{h}}\frac{\partial E}{\partial w}

\rho を仕込むことで、以前の h をある程度忘れるという式ですね。

Mac から乗り換えた:ASUS UF Dash F15 FX516PR

日記

乗り換えて 1 週間使ったので、レビューを。

乗り換えたのはコレ。

ASUSTek ゲーミングノートパソコン TUF Dash F15 FX516PR(Core i7-11370H/16GB・1TB/RTX 3070/1,920×1,080ドット (フルHD) (240Hz)/15.6インチ/日本語キーボード/Wifi6/ムーンライトホワイト)【日本正規代理店品】【あんしん保証】FX516PR-I7R3070ECW

ASUSTek ゲーミングノートパソコン TUF Dash F15 FX516PR(Core i7-11370H/16GB・1TB/RTX 3070/1,920×1,080ドット (フルHD) (240Hz)/15.6インチ/日本語キーボード/Wifi6/ムーンライトホワイト)【日本正規代理店品】【あんしん保証】FX516PR-I7R3070ECW

  • 発売日: 2021/01/27
  • メディア: Personal Computers

個人的評価

Mac から乗り換えるならこれが一番コスパ良いかも？

少なくともコストパフォーマンスで乗り換え選択を行うなら、これが個人的に一番しっくりくるという結論に至った。
概ね満足できるという評価です。

  • いい点
    • GeforceRTX 3000 番台（性能は RTX 2070 以上 RTX 2070 SUPER 以下）で、ヘビーでない限りはゲーム用途として申し分ない。
    • CPU も概ね満足。11世代 Core-i7 で何が不満なんだ…
    • 16GB メモリに、1T ストレージ。普通に使うのには支障がない。
    • テンキーが無い
    • この性能でこの値段は何だ！？
  • 悪い点
    • 静音か？と言われれば疑問は残る。GPU ぶん回すとかしなければ静音。
    • ディスプレイのリフレッシュレートが 200 超えるのに、搭載 Geforece はリミッターがあるのか、144Hz 位が良いところ…（ちょい勿体ない）

因みに、スペックだけで評価を見る場合はこちらのレビューがおすすめ

ASUS TUF Dash F15 FX516PRレビュー｜RTX 3070搭載ゲーミングノート｜ゲーミングPCログ

満足できる人

  • X86-64 CPU が必要で、かつ Mac から手ごろな値段で代わりに使えるマシンを模索している人。
  • ミドルレンジクラスでゲームをする人。
  • 開発者など。
  • 見た目のセンスより開発しやすいことが重要と割り切れる人

おすすめできない人

  • 経理とか数字をやたら打つ人
  • インストールは DVD からでないと…というアンチオンラインストア派
  • 事務系作業する人（ゲーミングPCにそもそも合わない）
  • Mac の見た目のセンスが良ーんだろーがという人

感想：なぜ Mac からの乗り換えに適してるか

Mac Book Pro 15inch 使ってた人は以下の内容に同意してくれるはずだ。

  • 分厚いPCは勘弁（DVDドライブとか邪魔。デスクトップで見ればいいし）
  • トラックパッドマウスに触ってフォーカス移動とか本気で要らない。むしろブチギレ案件
  • 15 インチ以上のディスプレイくれよ
  • メモリは 16G は必須
  • ストレージは多いに越したことはない

というもの。

残念ながら、このマシンは Mac より薄くはなく、ほかの Windows ノートよりはマシといったところ。
ではなぜおすすめできるかというと

コスパ

CPU/メモリ容量/ストレージ容量/グラボ これら合わせて 20 万ちょっとに収まるのは、コスパが良いといって差し支えない。
Asus は全体的にコスパは高め。

テンキーがない

これは経理とか一部の「数字をやたら叩くお仕事の人」には辛いかもしれないが、正直プログラマーにしてみれば利点でしかない。
むしろテンキーなんてものは邪魔でしかないと断じる。

  • ノートパソコンはそもそも面積に限界がある。
  • テンキーが入ると普通のキーはそれに押され、レイアウト上、中央から左寄りになってしまう。

さぁ、ここでプログラマーや開発者諸君の、「文字スペースを打つときに手首を置きたい」という要望があるとどうなるか？
打ちたいキーが左にずれる。なら右手首を置きたい場所には何がある…？

トラックパッドとかいう最も邪魔な機能がある

これである。

対抗馬

金に糸目を受けないという条件があるのなら、Dell の XPS 15 なども良いかもしれない。
比較するとこんな感じになる

  • XPS 15 の方が薄い
  • XPS 15 は 1TB ストレージを選択すると 30 万に突入する
  • それ以外の性能はおおよそ トントン

コスパを取るか薄さ（の代わりに高額）を取るか…

他の対抗馬としては

  • HP の Envy シリーズ：こちらも XPS シリーズと同じで、薄さでは勝ってるがディスク容量を求めると値段が跳ね上がる…。
  • Microsoft Surface シリーズ：メモリ 16 G以上にするなら 30 万近くになるんだ…薄いんだけどさ…
  • VAIO Z シリーズ：グラボ積んでなくていいならとてもいいかも？（個人的に Tensor を GPU で走らせたいので見送った）

…因みに HUAWEI の mate book シリーズは安くて薄いのだけど、米国繋がりで火中の栗感があって申し訳ないが避けた…