投資信託記録アプリのアップデート

white-azalea.hatenablog.jp

コレの続き。

github.com

アプリをアップデート。

• 口数の追加（よく見るこの数字）
  
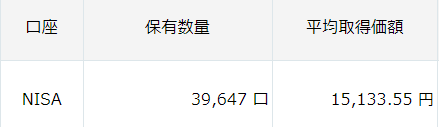
• 最新の合計資産価値 を更新したとき、各購入記録の「資産価値」を更新するロジックを、「口数」ベースで割り振るよう修正。

自分は積み立て NISA じゃなくて普通の NISA なんで、原則的に売ること前提の機能だね。

三次元グラフを書いてみるテスト

ちょっとやってみた感じです。

import numpy as np

x,y = np.mgrid[10:100:2, 10:100:2]
pos = np.empty(x.shape + (2,))

pos[:, :, 0] = x
pos[:, :, 1] = y

np.mgrid[10:100:2, 10:100:2] で x, y にグリッドなデータを生成させます。
この形状は、 10 起点で 100 未満まで 2 ステップで生成します。（データ数は 1 軸 45 個）

x.shape は (45, 45) で、x, y はそれぞれこんな形状になります。

 array([[10, 10, 10, ..., 10, 10, 10],
       [12, 12, 12, ..., 12, 12, 12],
       [14, 14, 14, ..., 14, 14, 14],
       ...,
       [94, 94, 94, ..., 94, 94, 94],
       [96, 96, 96, ..., 96, 96, 96],
       [98, 98, 98, ..., 98, 98, 98]])

array([[10, 12, 14, ..., 94, 96, 98],
       [10, 12, 14, ..., 94, 96, 98],
       [10, 12, 14, ..., 94, 96, 98],
       ...,
       [10, 12, 14, ..., 94, 96, 98],
       [10, 12, 14, ..., 94, 96, 98],
       [10, 12, 14, ..., 94, 96, 98]])

作成した pos はこの時点で

(45, 45, 2)
array([[[10., 10.],
        [10., 12.],
        [10., 14.],
        ...,
        [10., 94.],
        [10., 96.],
        [10., 98.]],

       [[12., 10.],
        [12., 12.],
        [12., 14.],
        ...,
        [12., 94.],
        [12., 96.],
        [12., 98.]],

       [[14., 10.],
        [14., 12.],
        [14., 14.],
        ...,
        [14., 94.],
        [14., 96.],
        [14., 98.]],

       ...,
show more (open the raw output data in a text editor) ...

        [98., 12.],
        [98., 14.],
        ...,
        [98., 94.],
        [98., 96.],
        [98., 98.]]])

まさに座標ですね。
ここにデータを肉付けします

from scipy.stats import multivariate_normal

rv = multivariate_normal([50, 50], [[100, 0], [0, 100]])
z = rv.pdf(pos)

multivariate_normal の引数を見ていくと、z,y ともに平均値 50、[[100, 0], [0, 100]] は 分散共分散行列(後述に詳細。分散100, 共分散0)
この時の z はこんな感じになっている。

(45, 45)
array([[1.79105293e-10, 3.90713230e-10, 8.18909735e-10, ...,
        3.33805656e-11, 1.35715252e-11, 5.30141552e-12],
       [3.90713230e-10, 8.52330075e-10, 1.78642887e-09, ...,
        7.28187781e-11, 2.96059059e-11, 1.15648909e-11],
       [8.18909735e-10, 1.78642887e-09, 3.74423972e-09, ...,
        1.52623463e-10, 6.20520695e-11, 2.42392656e-11],
       ...,
       [3.33805656e-11, 7.28187781e-11, 1.52623463e-10, ...,
        6.22126874e-12, 2.52937912e-12, 9.88045888e-13],
       [1.35715252e-11, 2.96059059e-11, 6.20520695e-11, ...,
        2.52937912e-12, 1.02836881e-12, 4.01709481e-13],
       [5.30141552e-12, 1.15648909e-11, 2.42392656e-11, ...,
        9.88045888e-13, 4.01709481e-13, 1.56918905e-13]])

それぞれの位置に一つづつ値が入っている形かな。
これを作画すると

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure(dpi=100)
ax = Axes3D(fig)

ax.plot_wireframe(x, y, z)

ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x, y)')

ax.ticklabel_format(style='sci', axis='z', scilimits=(0, 0))

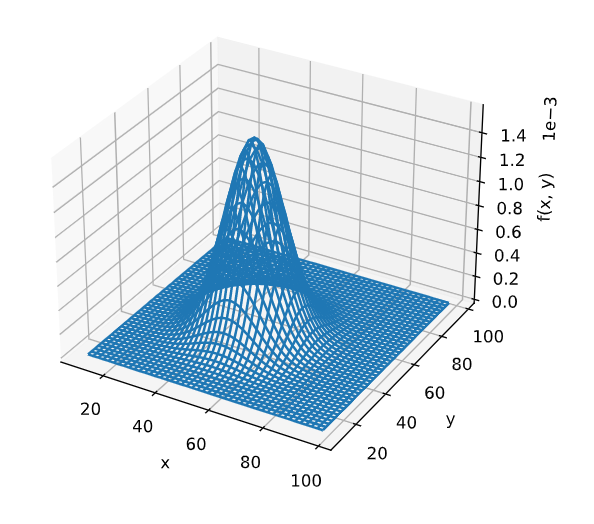
うーんかっこいい

分散共分散行列

分散共分散行列とは、 と の2つの数列があり、こんな値を持ってるとします

としたとき、平均値 E は

で、偏差(実値 - 平均)を取ると

で、各分散を考えると

共分散 は の様に記述し

要するに は A,B の偏差をかけた平均= 共分散

で、分散共分散の定義は

で、当てはめて

という形になります。

Salesforce Platform Developer の資格維持

Salesforce の資格は一度とったら終了ではなく、定期的にスキルをアップデートしなければならないご様子。
これは、Trailhead にログインして、自分のステータスを見るときに

こんな感じで表示される。
更新に関しては下記のバッチを取ればいいらしい

trailhead.salesforce.com

Apex

WITH SECURITY_ENFORCED

SOQL のケツにつけることができる修飾句。
SELECT と FROM で列挙されている項目のアクセス権限がチェックできる。

権限がないと例外を起こすとのこと。
これ項目のアクセス権限の事前チェックしなくても良くなる系？

※ 多態項目は原則サポートされません。例外として Owner, CreatedBy, LastModifiedBy は除外され、適用できるとのこと。

プラットフォームイベントの再開

プラットフォームイベントを Apex トリガで受け取る際、何らかの理由（デバッグ中だったとか）でトリガをスキップしたい場合、これまではトリガを無効にしてイベント実行→復帰しなければならず、その間のイベントは永久にトリガで処理できなくなっていました。
が、 Winter21 からは任意の一時停止、復帰の他、復帰時に停止中に流れたイベントを再処理させることができるようになったと。

「プラットフォームイベント」のトリガ詳細から「Suspend」「Resume」でこれが可能になるとのこと。

ロック解除済みパッケージのコードカバー率

Winter '21 以降で作成されたパッケージバージョンのうち、このコードカバー率を満たさないものは、スクラッチ組織と Sandbox にしかインストールできません。Winter ’21 より前にリリース済み状態に昇格されたロック解除済みパッケージバージョンは、コードカバー率要件の対象外です。

昇格って言い回しが謎だけど多分「リリース」かな。
まぁ元より新しい物作るときは 75% のカバー率を要求されるので、得てしてこんなものかなと…

Messaging.CustomNotification

Messaging.CustomNotification クラスが新規に入った。
ユーザに簡単に通知を投げる手段のようだ。

[Salesforce]カスタム通知機能を使用 - コードワールド

プラットフォームイベントメッセージの公開後の Apex コールアウトの実行

これまでは DML （DB でいう CreateUpdateDelete）とか処理した後でコールアウト（外部APIのHTTP呼び出しの事）を実行できず、プラットフォームイベントも同様に DML とみなされていた。
が、Winter '21 から「すぐに公開」としていれば、DML操作とはみなされなくなる模様。

…あんま使った記憶ないけど（汗

LWC

track アノテーションの一部不要化

html 上で利用する変数に @track を入れておかないと、値の変更時に画面に適用されなかった…は過去の話。
Spring ’20 以降では、配列でなければ原則不要になりました。

…ってことは原則全変数で値の監視してるって事かな… Proxy オブジェクトラップとかデバッグ時に追いづらくて嫌なんやけど（汗

Lightning Message Service

Summer ’20 でGA

DOM (これは HTML のDOMな)全体の VF/Aura/LWC で通信を行う仕組み。
LWC で画面上の値を変更＆保存したときに「おらーVF！Aura！おめーらが参照してるデータ更新されたで！」みたいな通知できるわけだ。

サンプルは Component Library らしい

Lightning Web コンポーネントのユーザ権限の確認

カスタム権限を設定しているとき、そのカスタム権限が現在のユーザで利用可能であるかどうかをチェックする機構が入ったとのこと。
因みにカスタム権限は これ 参照。

標準権限

import hasPermission from '@salesforce/userPermission/StandardPermissionName';

カスタム権限

import hasPermission from '@salesforce/customPermission/namespace__CustomPermissionName';

標準とカスタムで取得元違うの何なの…

項目レベルとオブジェクトレベルのセキュリティや安全なナビゲーション演算子

Security.StripInaccessible

Security.StripInaccessible を使って、指定した権限の無い項目や行をフィルタ出来る。

SObjectAccessDecision securityDecision =
       Security.stripInaccessible(AccessType.UPDATABLE,
             [SELECT Name, BudgetedCost, ActualCost FROM Campaign]
             );
// Print stripped records
for (SObject strippedAccount : securityDecision.getRecords()) {
    System.debug(strippedAccount);
}

簡易的な null の扱い

JavaScript から Apex に持ってきたのかな…これは使い勝手がいい

a?.b // Evaluates to: a == null ? null : a.b

確率周りの勉強続き

確率変数が複数あるときの確率分布

white-azalea.hatenablog.jp

これの続き

同時確率分布

ある薬の治験に 40 人が集まり各データ

	A型	B型	O型	AB型	合計
男性	10	4	4	2	20
女性	8	2	8	2	20

で発生確率は人数的に確率はこんな感じ

	A型	B型	O型	AB型	合計
男性	0.25	0.1	0.1	0.05	0.5
女性	0.2	0.05	0.2	0.05	0.5
計	0.45	0.15	0.3	0.1	1

で、血液型 X 性別 Y としたときにそれぞれが特定の値を取るときの確率を表したものを「同時確率分布」と言う。 血液型が , 性別が を取るときの確率を表す関数を同時確率関数という。

例えば、A 型かつ男性 と取得できる。
また、 の時(または )固定の時の確率分布を「周辺確率分布」といい

てな感じで周辺確率関数を定義できる。
仮に、A型と割り切って( ) を考えると、 Y は性別なので、男性女性の合計なので、合計確率 0.45 と。

条件付き確率関数

を与えたときの である確率（条件付き確率関数）を

と記述する。

条件付き期待値

前述の条件付き確率関数に、期待値を取ったもの。
を与えたときの Y の 条件付き期待値 を

と記述する。

ゾンビウイルスが蔓延したと仮定して何日で全滅するか

ゾンビウイルスが蔓延したと仮定して、どれくらいの期間で死滅するか考えてみる。
これは要するに生存者は何日立てこもれば生存できるのかという事である。

大前提として 「生物としての肉体的変質を伴わない前提」 としたい。
例えばバイオハザードの G ウイルスみたいに、「生物を遺伝子レベルで書き換えてデタラメに進化させてしまう」みたいな話になってくると、体の構造なんて予測もつかないので想定すらできない。

もう一つの前提は 生物としての代謝は変わらない という前提だ。
良くバイオの映画だと、感染したら速攻腐ったような肌色になって、なんなら腐った体で襲い掛かってくる。
そもそも代謝が停止していて栄養分が筋肉に渡ってないなら、筋肉を動かすエネルギーなんて全身に届くハズもない。
つまり体が動くハズがないので、あくまで感染したら食う以外の思考が全部ぶっ飛ぶ前提とする。

「食う事しか考えない」最もアホな型

実写映画バイオハザードの一番最初の作品で、AI が「食う事よ」と言っていた。
まさかと思うが「飲まない」とした場合、どうなるか？

結論: 1 週間以内にゾンビは全滅する（ゾンビの死因は脱水症状）

人は発汗だけで1日 1.5～2リットル ( 1日に必要な水分量は？ | BRITA® )ここにトイレ等も含めると、普通に 2.8～3 リットルは最低限欲しい。
が、人肉でこれを補給する場合、人体の水分の割合は 7 割で、ここから 3 リットルの水を得ようとすると 4.29kg もの肉を食うことに…

見れば分かるが、こんな質量の肉1日に食えません…当然消化だってしなきゃいけないし排泄だって必要ですもん…
ということで、「水を飲む」ことを止めたゾンビは早晩行動不能に陥る。

確率周りの定義

確率周りの定義

• 確率変数: 確率が割り当てられる変数。サイコロなら $\frac{1}{6}$ の確率が確率変数(1-6 で変動)に割り当てられてると言える。
• 現実値: 確率変数の取りえる値。サイコロなら 1-6
• 離散確率変数、連続確率変数: 確率変数の値の範囲が有限数の場合を 離散確率変数 、そうでないときに 連続確率変数 という。

確率分布関数

確率変数 X が実数 x いかになる確率の事。離散確率変数は $F(X)$ で記述し、定義は

確率密度関数

連続確率変数の場合は、分布関数の導関数を密度関数(確率密度関数)という。

平均の確率での表し方

確率変数を X とし、平均（期待値）を $E(X)$ で表すとこんな感じで表す。

Σ 事象 x × 発生確率 f(x)

と読み替えると分かりやすいか

各種分布

• 一様分布 : サイコロなどはすべての確率変数が一様に $\frac{1}{6}$ の確率で、このように一様なさまを一様分布という
• ベルヌーイ分布 : 結果が2択の分布をベルヌーイ分布という。コインとか。尚、二択の結果が出る試行を ベルヌーイ試行 というそうな
• 二項分布 : ベルヌーイ試行を独立に n 回繰り返したときの成功回数を確率変数とする分布。
  全住民の 5% がある感染症に罹患していて、その住民の中から無作為に 500 人抽出した。この抽出した 500 人のうち、罹患者が紛れ込む人数の分布等。

二項分布の例

# 500 人抽出, 5% の罹患率, 100 回抽出
x = np.random.binomial(500, 0.05, 100)
x.shape  # (100,)

ベイズ定理を使ってみる

を結果事象、 をその原因事象としたとき、「 の原因が に起因したものである確率 」を以下の式で示す

は事象 が起きた後の の発生確率(事後確率)。
この時 は事象 が発生する前の事象 の確率(事前確率)。
は が発生した際に、 が原因である確率(尤度)。

これは原因が一つであることを前提とした式で、原因が複数 ( 等)ある場合の一般式は

実計算

• ある病気 X に感染している可能性は 0.1 % である。
• ある PCR 検査したとき、感染している患者は 99% の確率で陽性反応が出る。
• 健康な人に PCR 検査を行った時、3% の確率で陽性反応が誤検知される。
• あなたは陽性反応が出ている。実際に感染している可能性は？

事象から定義してみる。

• A : X に感染している
• B : PCR が陽性を示す

とすると、ベイズ定理に当てはめると

因果的には PCR (B) → 感染？ (A) なので、AB読み替えで

結論: 約 3.2% の確率で感染しています。
と、いうように扱うことができた。