三次元グラフを書いてみるテスト

ちょっとやってみた感じです。

import numpy as np

x,y = np.mgrid[10:100:2, 10:100:2]
pos = np.empty(x.shape + (2,))

pos[:, :, 0] = x
pos[:, :, 1] = y

np.mgrid[10:100:2, 10:100:2] で x, y にグリッドなデータを生成させます。
この形状は、 10 起点で 100 未満まで 2 ステップで生成します。（データ数は 1 軸 45 個）

x.shape は (45, 45) で、x, y はそれぞれこんな形状になります。

 array([[10, 10, 10, ..., 10, 10, 10],
       [12, 12, 12, ..., 12, 12, 12],
       [14, 14, 14, ..., 14, 14, 14],
       ...,
       [94, 94, 94, ..., 94, 94, 94],
       [96, 96, 96, ..., 96, 96, 96],
       [98, 98, 98, ..., 98, 98, 98]])

array([[10, 12, 14, ..., 94, 96, 98],
       [10, 12, 14, ..., 94, 96, 98],
       [10, 12, 14, ..., 94, 96, 98],
       ...,
       [10, 12, 14, ..., 94, 96, 98],
       [10, 12, 14, ..., 94, 96, 98],
       [10, 12, 14, ..., 94, 96, 98]])

作成した pos はこの時点で

(45, 45, 2)
array([[[10., 10.],
        [10., 12.],
        [10., 14.],
        ...,
        [10., 94.],
        [10., 96.],
        [10., 98.]],

       [[12., 10.],
        [12., 12.],
        [12., 14.],
        ...,
        [12., 94.],
        [12., 96.],
        [12., 98.]],

       [[14., 10.],
        [14., 12.],
        [14., 14.],
        ...,
        [14., 94.],
        [14., 96.],
        [14., 98.]],

       ...,
show more (open the raw output data in a text editor) ...

        [98., 12.],
        [98., 14.],
        ...,
        [98., 94.],
        [98., 96.],
        [98., 98.]]])

まさに座標ですね。
ここにデータを肉付けします

from scipy.stats import multivariate_normal

rv = multivariate_normal([50, 50], [[100, 0], [0, 100]])
z = rv.pdf(pos)

multivariate_normal の引数を見ていくと、z,y ともに平均値 50、[[100, 0], [0, 100]] は分散共分散行列(後述に詳細。分散100, 共分散0)
この時の z はこんな感じになっている。

(45, 45)
array([[1.79105293e-10, 3.90713230e-10, 8.18909735e-10, ...,
        3.33805656e-11, 1.35715252e-11, 5.30141552e-12],
       [3.90713230e-10, 8.52330075e-10, 1.78642887e-09, ...,
        7.28187781e-11, 2.96059059e-11, 1.15648909e-11],
       [8.18909735e-10, 1.78642887e-09, 3.74423972e-09, ...,
        1.52623463e-10, 6.20520695e-11, 2.42392656e-11],
       ...,
       [3.33805656e-11, 7.28187781e-11, 1.52623463e-10, ...,
        6.22126874e-12, 2.52937912e-12, 9.88045888e-13],
       [1.35715252e-11, 2.96059059e-11, 6.20520695e-11, ...,
        2.52937912e-12, 1.02836881e-12, 4.01709481e-13],
       [5.30141552e-12, 1.15648909e-11, 2.42392656e-11, ...,
        9.88045888e-13, 4.01709481e-13, 1.56918905e-13]])

それぞれの位置に一つづつ値が入っている形かな。
これを作画すると

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure(dpi=100)
ax = Axes3D(fig)

ax.plot_wireframe(x, y, z)

ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x, y)')

ax.ticklabel_format(style='sci', axis='z', scilimits=(0, 0))

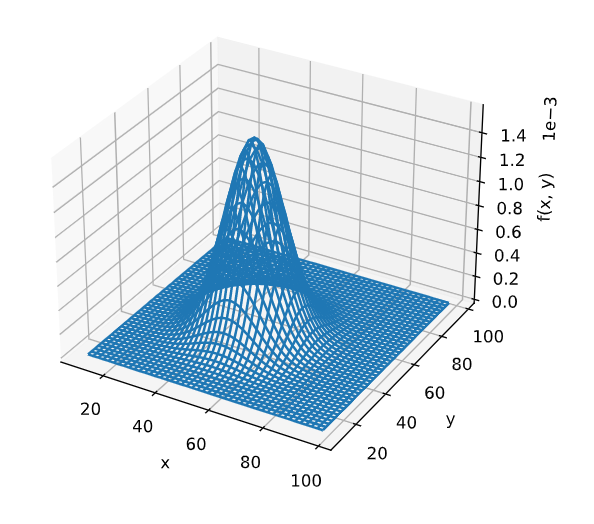
f:id:white-azalea:20210826215900p:plain