RNN で時系列データの予測をやってみる
この辺の続き
要するに次の値を予測してもらうという NN ですな
まずは結果から
正弦波にノイズを与えたデータが学習データ青で、先頭 10 件だけはそのまま、11 件目以降を 10 件づつ与えたデータから予測させて作ったグラフが黄色である。
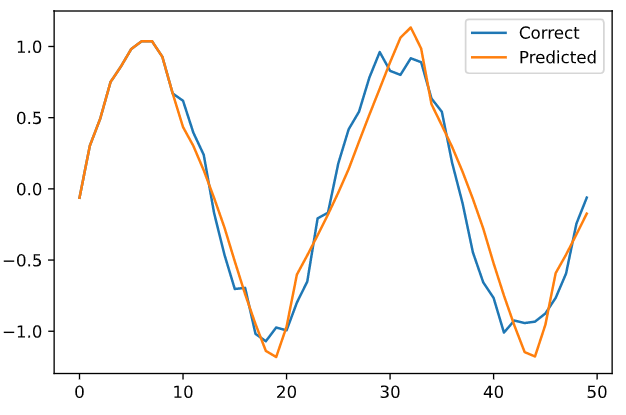
ん、まぁなんとなく正しそうな予感はする。
株価みたいな線形データならやれるだろうか…取り込めるデータは1系統なので、特定銘柄特化でならなりそうな気はするが…。
で、ソース。
学習データソースはこんな感じ。
import numpy as np import matplotlib.pyplot as plt %matplotlib inline # ダミー学習データ(X軸範囲) sin_x = np.linspace(-2 * np.pi, 2 * np.pi) # ノイズを載せる sin_y = np.sin(sin_x) + 0.1 * np.random.randn(len(sin_x))
これを学習するにあたってデータ形状変換
n_time = 10 n_in = 1 # 入力層ニューロン数 n_mid = 20 # 中間層ニューロン数 n_out = 1 # 出力層ニューロン数 # 学習データ n_sample = len(sin_x) - n_time input_data = np.zeros((n_sample, n_time, n_in)) correct_data = np.zeros((n_sample, n_out)) for i in range(0, n_sample): input_data[i] = sin_y[i:i+n_time].reshape(-1, 1) correct_data[i] = sin_y[i+n_time : i+n_time+1] # 一度に食わせるデータは n_time 個数分 # データ形式的には # input_data[元データ件数 - 学習する時間][1単位時間進んだデータ][時間単位データ] # input_data[0] = 学習データの先頭~n_time 分のデータ # input_data[0][0] = [先頭データ] # input_data[0][1] = [先頭+1 のデータ] # correct_data は 1 データだけずらした値
要するに対応付けは「input_data[0] = 先頭から n_time 件のデータ : correct_data[0] = n_time + 1 時刻の値」で学習させる
活性関数にはオーソドックスに
を採用。
class RnnBaseLayer: def __init__(self, n_upper, n): self.w = np.random.randn(n_upper, n) / np.sqrt(n_upper) self.v = np.random.randn(n, n) / np.sqrt(n) self.b = np.zeros(n) def forward(self, x, prev_y): u = np.dot(x, self.w) + np.dot(prev_y, self.v) + self.b self.y = np.tanh(u) def backword(self, x, y, prev_y, grad_y): delta = grad_y * (1 - y**2) self.grad_w += np.dot(x.T, delta) self.grad_v += np.dot(prev_y.T, delta) self.grad_b += np.sum(delta, axis=0) self.grad_x = np.dot(delta, self.w.T) self.grad_prev_y = np.dot(delta, self.v.T) def reset_sum_grad(self): self.grad_w = np.zeros_like(self.w) self.grad_v = np.zeros_like(self.v) self.grad_b = np.zeros_like(self.b) def update(self, eta): self.w -= eta * self.grad_w self.v -= eta * self.grad_v self.b -= eta * self.grad_b class OutputLayer: def __init__(self, n_upper, n): self.w = np.random.randn(n_upper, n) / np.sqrt(n_upper) self.b = np.zeros(n) def forward(self, x): self.x = x u = np.dot(x, self.w) + self.b self.y = u def backword(self, t): delta = self.y - t self.grad_w = np.dot(self.x.T, delta) self.grad_b = np.sum(delta, axis=0) self.grad_x = np.dot(delta, self.w.T) def update(self, eta): self.w -= eta * self.grad_w self.b -= eta * self.grad_b
で、実際の実装が
epochs = 51 batch_size = 8 interval = 5 eta = 0.001 # 学習 rnn_layer = RnnBaseLayer(n_in, n_mid) out_layer = OutputLayer(n_mid, n_out) def train(x_mb, t_mb): y_rnn = np.zeros((len(x_mb), n_time + 1, n_mid)) prev_y = y_rnn[:, 0, :] for i in range(n_time): x = x_mb[:, i, :] rnn_layer.forward(x, prev_y) y = rnn_layer.y y_rnn[:, i + 1, :] = y prev_y = y out_layer.forward(y) # 逆伝播 out_layer.backword(t_mb) grad_y = out_layer.grad_x rnn_layer.reset_sum_grad() for i in reversed(range(n_time)): x = x_mb[:, 1, :] y = y_rnn[:, 1+1, :] prev_y = y_rnn[:, i, :] rnn_layer.backword(x, y, prev_y, grad_y) grad_y = rnn_layer.grad_prev_y # パラメータ更新 rnn_layer.update(eta) out_layer.update(eta) # 予測 def predict(x_mb): prev_y = np.zeros((len(x_mb), n_mid)) for i in range(n_time): x = x_mb[:, i, :] rnn_layer.forward(x, prev_y) y = rnn_layer.y prev_y = y out_layer.forward(y) return out_layer.y # エラー計測 def get_error(x, t): y = predict(x) return 1.0 / 2.0*np.sum(np.square(y - t)) n_batch = len(input_data) for i in range(epochs): # create rand indexes index_rand = np.arange(len(input_data)) np.random.shuffle(index_rand) for j in range(n_batch): # get learn data and corrects mb_index = index_rand[j*batch_size : (j+1)*batch_size] x_mb = input_data[mb_index, :] t_mb = correct_data[mb_index, :] train(x_mb, t_mb) # calc err error = get_error(input_data, correct_data) # show state if i % interval == 0: print(f'Epoch: {i + 1} / {epochs} , Error: {error}') predicted = input_data[0].reshape(-1).tolist() for i in range(n_sample): x = np.array(predicted[-n_time:]).reshape(1, n_time, 1) y = predict(x) predicted.append(float(y[0, 0])) plt.plot(range(len(sin_x)), sin_y.tolist(), label='Correct') plt.plot(range(len(predicted)), predicted, label='Predicted') plt.legend() plt.show()
やってみれば分かるが、誤差は結構出る。
ノイズのある状況で次の値を予測するので、そこらへんはご容赦って感じではあるかな。
現実的にはノイズは常に存在するので、ここはあきらめモードではないかと思う。