最急降下法を使用して、近似線を引いてみる

やっていることは前回とほぼ同様。
ただしこちらでは偏微分を使って複数のパラメータを計算している。

white-azalea.hatenablog.jp

目標とすべき線が

def actual(x):
    """目指すべき線"""
    return 0.6 * x + 4

で、学習データセットを以下の様に設定してみる。

data_set = [(x, actual(x) + random.randint(-5, 5)) for x in range(-100, 100)]

緑が学習データで、青線が理想の線。
ばらけ方は悪いけど、この辺がテストデータ

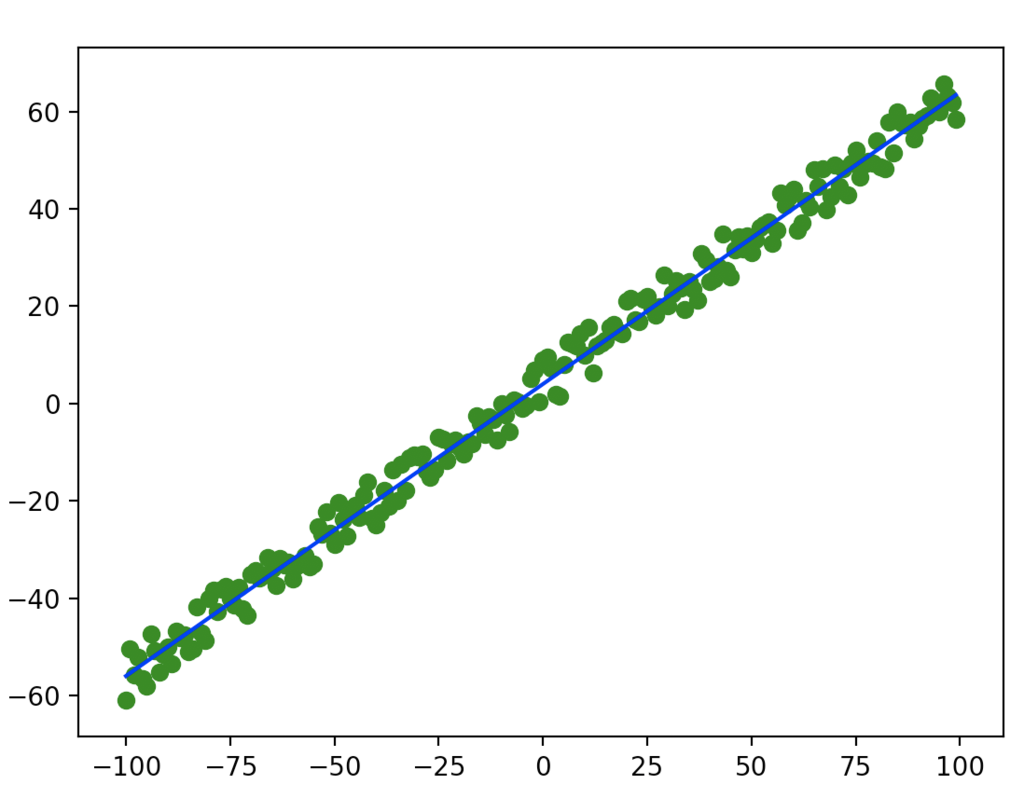
そして求めるべきパラメータは、前後変化するので引数で受け取る様にして外だしに。

# weight のパラメータを使って actual 同様の計算をする
def func(x, weight):
    return weight[0] * x + weight[1]

あとのやることは対して変わらない。
微分関数を用意。

def numerical_gradient(f, weight):
    """偏微分式にアップデート"""
    h = 1e-4
    grad = []

    for i in range(0, len(weight)):
        cpy1 = weight[:]
        cpy2 = weight[:]
        cpy1[i] = cpy1[i] + h
        cpy2[i] = cpy2[i] - h
        fhx1 = f(cpy1)
        fhx2 = f(cpy2)
        grad.append((fhx1 - fhx2) / (2 * h))
    return grad

ただし、今回は重み付けパラメータの値を個別に微分し、微分値を応答に含む様にしている。
偏微分て要するに他のパラメータを全て定数とみなして微分することなので、やっている論理は一緒。

損失関数を用意して、その損失関数に不足するパラメータを設定する。

def loss(func, data, actual, weight):
    calc = func(data, weight)
    return (actual - calc)**2

今回は 0 に近づけるのではなくて、微妙にブレた各数字データに近づける。

lern = 0.00001
weight = [-2, 3]  # 最初の重みは適当
for n in range(1000):
    for data in data_set:
        x, y = data
        loss_func = lambda w: loss(func, x, y, w)
        grads = numerical_gradient(loss_func, weight)
        weight = [weight[0] - grads[0] * lern, weight[1] - grads[1] * lern]

初期の weight は明らかに伸びる向きが間違ってる。
これは補正がかかることを確認するためにわざと行なっている。

その上で赤線プロットするとこのようになる。
（黄色は学習前で、赤は学習後。きちんと学習しているようである）

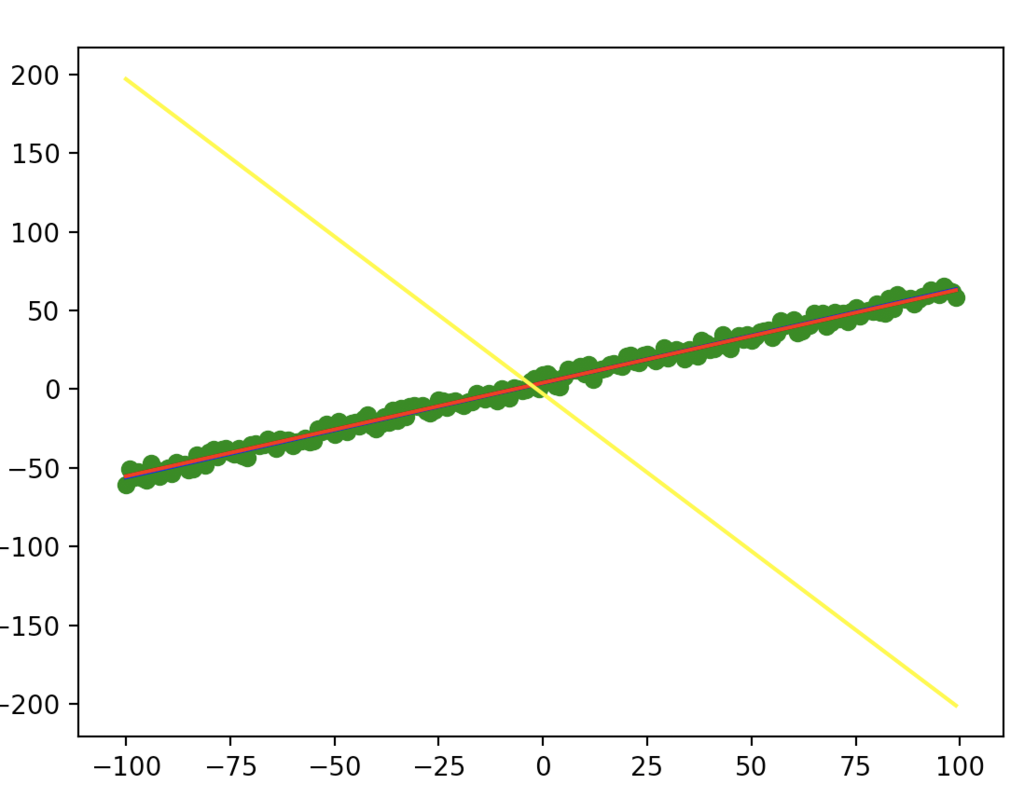
ここでもう一声。
損失関数と呼んではいるが、これは目的関数とも言えるので、その原義（下記）に従って、損失計算を作り直してみる。

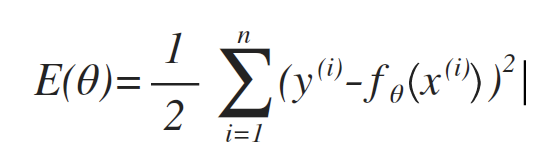
※ y(i) はデータはデータの y 軸の値。fθは今回で言う所の func(?, weight)の意味で、θ=weight 値。

lern = 0.000002
weight = [-2, 3]  # 最初の重みは適当
for n in range(5000):
    def error(weight):
        all_err = 0.0
        for data in data_set:
            x, actual_y = data
            all_err += (actual_y - func(x, weight))**2
        return all_err / 2.0
    grads = numerical_gradient(error, weight)
    weight = [weight[0] - grads[0] * lern, weight[1] - grads[1] * lern]

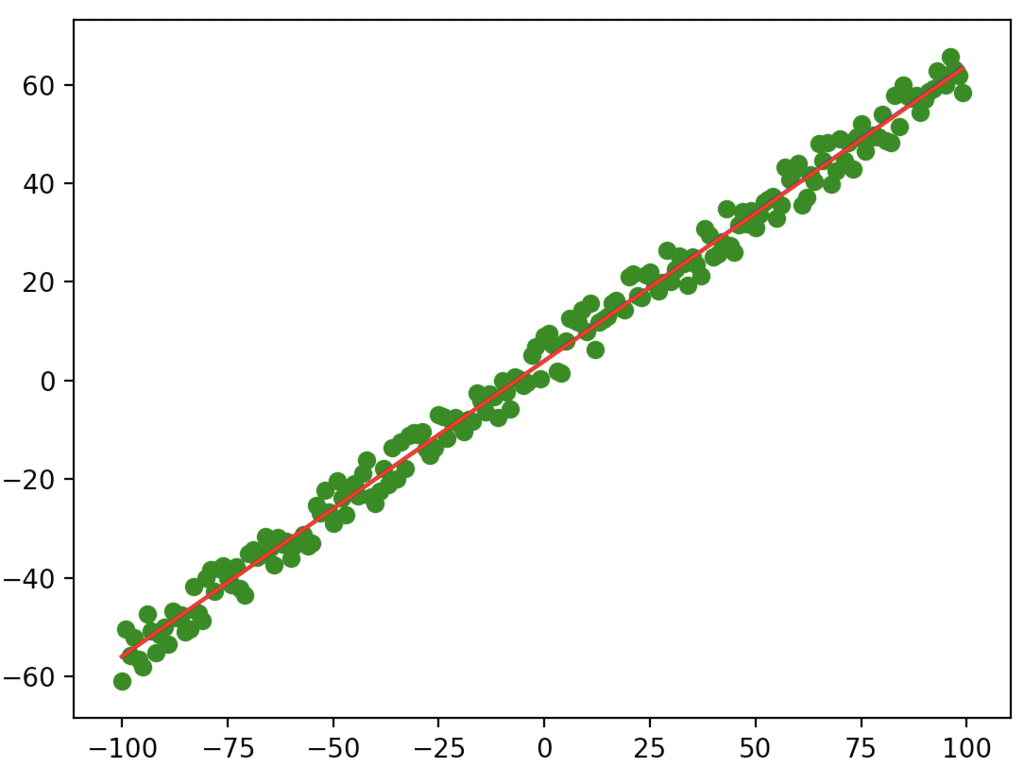
ループなどは一部弄ったが、ループは明らかに少ない回数でいい精度の数字が出てきた。