過学習対策あれこれ
前回わざと過学習させてみたわけだが、そもそも学習の打ち切りはやたらと難しいハズだ。
あの時はデータセットが 200 位しかないし、ニューロンの数も限られていたといえる。
しかし、現実には大量のデータセットがあるだろうし、学習時間はそこそこかかるだろうと思われる。
例えば1回の学習だけで数時間かかるとする。
それを見て、じゃぁどの位で打ち切るか?2週目開始までにどれだけ待つ必要があるだろう?
要するに学習の打ち切りを判断するのはちょとどころでは難しいと予測できる。
ということで、今回はやり方を変えてみる。
まずは前回の誤差を見てみよう。
Epoch: 0 / 1000, Err_train: 1.1043634751935245, Err_test: 1.0623824378086812 Epoch: 100 / 1000, Err_train: 0.04227735559583767, Err_test: 0.13396243782658682 Epoch: 200 / 1000, Err_train: 0.018747407955545834, Err_test: 0.12865441586002588 Epoch: 300 / 1000, Err_train: 0.004991569690202153, Err_test: 0.218183645593179 Epoch: 400 / 1000, Err_train: 0.002959841289188, Err_test: 0.25887483170314346 Epoch: 500 / 1000, Err_train: 0.001493562533847086, Err_test: 0.3049230574592406 Epoch: 600 / 1000, Err_train: 0.0010474962034239849, Err_test: 0.3333645685971381 Epoch: 700 / 1000, Err_train: 0.0007757803305818819, Err_test: 0.3506614397003805 Epoch: 800 / 1000, Err_train: 0.0006128411251375161, Err_test: 0.36719589756963056 Epoch: 900 / 1000, Err_train: 0.0004995183637277335, Err_test: 0.37831813699595335

最終的に過学習のせいで 0.4 目指してエラーが広がっている。
モノは試しに RMSProp を導入してみた。
式は過去記事のものを利用。
roh = 0.95 class RMSNeuron(Neuron): def __init__(self, n_upper, n, activation_function, differential_function): super().__init__(n_upper, n, activation_function, differential_function) self.h_w = np.zeros((n_upper, n)) + 1e-8 self.h_b = np.zeros((n)) + 1e-8 def update(self): # ここだけ更新 self.h_w = (self.h_w * roh) + (1 - roh) * (self.grad_w * self.grad_w) self.h_b = (self.h_b * roh) + (1 - roh) * (self.grad_b * self.grad_b) self.w -= eta / np.sqrt(self.h_w) * self.grad_w self.b -= eta / np.sqrt(self.h_b) * self.grad_b class Output(RMSNeuron): pass class Middle(RMSNeuron): def backword(self, grad_y): delta = self.differential_function(grad_y, self.y) self.grad_w = self.x.T.dot(delta) self.grad_b = delta.sum(axis = 0) self.grad_x = delta.dot(self.w.T) return self.grad_x # ニューロン初期化 mid_layer1 = Middle(n_in, n_mid, relu_func, relu_func_dash) mid_layer2 = Middle(n_mid, n_mid, relu_func, relu_func_dash) outputs = Output(n_mid, n_out, soft_max, soft_max_dash) exec()
結果が
Epoch: 0 / 1000, Err_train: 1.1000068284857787, Err_test: 1.105102282860116 Epoch: 100 / 1000, Err_train: 0.0004723302009342129, Err_test: 0.25285731779944576 Epoch: 200 / 1000, Err_train: 2.435419747198503e-05, Err_test: 0.41570733582516095 Epoch: 300 / 1000, Err_train: 1.6498331127020632e-07, Err_test: 0.42415464268234687 Epoch: 400 / 1000, Err_train: 3.2775216891847647e-06, Err_test: 0.424167001320326 Epoch: 500 / 1000, Err_train: 1.7252434605417651e-06, Err_test: 0.42416032411453786 Epoch: 600 / 1000, Err_train: -9.588821783186093e-08, Err_test: 0.42416031798981263 Epoch: 700 / 1000, Err_train: 1.9298299962666904e-07, Err_test: 0.424160335489329 Epoch: 800 / 1000, Err_train: -2.7639660886741467e-08, Err_test: 0.42416031479869326 Epoch: 900 / 1000, Err_train: -9.780188673424984e-08, Err_test: 0.4241603145452869

ちょwwwww
過学習広がったしwwww
アカンw これ学習係数は一方通行で減らさないとダメだコレw
初期段階で一気に学習進めると、一時的に学習係数に圧がかかって、緩やかになるのだけど、それ以降で物忘れによって学習係数が跳ね上がる。 そこに過学習が入ってヒャッハーされたことが見て取れる。
一方通行で学習係数増やさないとダメだこれは…。
次に、 以前軽めにやってみた AdaGrad を改めて入れてみる。
class AdaNeuron(Neuron): def __init__(self, n_upper, n, activation_function, differential_function): super().__init__(n_upper, n, activation_function, differential_function) self.h_w = np.zeros((n_upper, n)) + 1e-8 self.h_b = np.zeros((n)) + 1e-8 def update(self): # ここだけ更新 self.h_w += (self.grad_w * self.grad_w) self.h_b += (self.grad_b * self.grad_b) self.w -= eta / np.sqrt(self.h_w) * self.grad_w self.b -= eta / np.sqrt(self.h_b) * self.grad_b class Output(AdaNeuron): pass class Middle(AdaNeuron): def backword(self, grad_y): delta = self.differential_function(grad_y, self.y) self.grad_w = self.x.T.dot(delta) self.grad_b = delta.sum(axis = 0) self.grad_x = delta.dot(self.w.T) return self.grad_x # ニューロン初期化 mid_layer1 = Middle(n_in, n_mid, relu_func, relu_func_dash) mid_layer2 = Middle(n_mid, n_mid, relu_func, relu_func_dash) outputs = Output(n_mid, n_out, soft_max, soft_max_dash) exec()
Epoch: 0 / 1000, Err_train: 1.0970762378611862, Err_test: 1.100821175245513 Epoch: 100 / 1000, Err_train: 0.05217075232904391, Err_test: 0.0757559293383057 Epoch: 200 / 1000, Err_train: 0.039067828663485446, Err_test: 0.07011980289918843 Epoch: 300 / 1000, Err_train: 0.03260663213844774, Err_test: 0.07246301952164647 Epoch: 400 / 1000, Err_train: 0.028273638257845537, Err_test: 0.07608998682857775 Epoch: 500 / 1000, Err_train: 0.025032418817387023, Err_test: 0.08099753529235809 Epoch: 600 / 1000, Err_train: 0.02246872590189229, Err_test: 0.08555487978897107 Epoch: 700 / 1000, Err_train: 0.020359704011542124, Err_test: 0.09098390127806043 Epoch: 800 / 1000, Err_train: 0.018583431357822176, Err_test: 0.09611910360147138 Epoch: 900 / 1000, Err_train: 0.017049638551187313, Err_test: 0.10118114361161198
おーブレもないしすごい安定感w
後半になるほど学習係数に負荷がかかっていくので、最後の方は殆ど学習しなくなっています。 後は学習の丁度いい時期に負荷が一気に溜まったことで、その後の学習のブレ(波打ち)が減りましたね。
最後にドロップアウトもやってみる。
ドロップアウトは適当なニューロンを時折死滅させることで過学習を抑えるというもの。
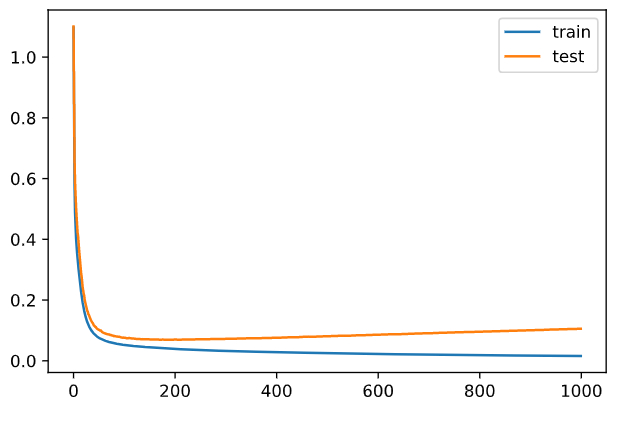
class Dropout: def __init__(self, dropout_rate): self.dropout_rate = dropout_rate def forward(self, x, is_train): if is_train: # ランダムにニューロンを選定して、その応答を 0 固定応答にする rand = np.random.rand(*x.shape) self.dropout = np.where(rand > self.dropout_rate, 1, 0) self.y = x * self.dropout else: self.y = (1 - self.dropout_rate) * x return self.y def backward(self, grad_y): # 眠ってなかったニューロンにだけバックプロパゲーションを返す self.grad_x = grad_y * self.dropout return self.grad_x # ニューロン初期化 mid_layer1 = Middle(n_in, n_mid, relu_func, relu_func_dash) mid_layer2 = Middle(n_mid, n_mid, relu_func, relu_func_dash) drop_layer1 = Dropout(0.5) drop_layer2 = Dropout(0.5) outputs = Output(n_mid, n_out, soft_max, soft_max_dash) def forward_propagation(x, is_train): y = mid_layer1.forward(x) y = drop_layer1.forward(y, is_train) # 間にドロップアウト層を挟む y = mid_layer2.forward(y) y = drop_layer2.forward(y, is_train) # 間にドロップアウト層を挟む return outputs.forward(y) def back_propagation(t): u = outputs.backword(t) u = drop_layer2.backward(u) # 間にドロップアウト層を挟む u = mid_layer2.backword(u) u = drop_layer1.backward(u) # 間にドロップアウト層を挟む mid_layer1.backword(u) def exec(): train_err_x = [] train_err_y = [] test_err_x = [] test_err_y = [] for i in range(epoch): # 誤差測定 x_res = forward_propagation(X_train, False) err_train = get_err(x_res, y_train, n_train) y_res = forward_propagation(X_test, False) err_test = get_err(y_res, y_test, n_test) train_err_x.append(i) train_err_y.append(err_train) test_err_x.append(i) test_err_y.append(err_test) # 途中経過 if i % interval == 0: print(f'Epoch: {i} / {epoch}, Err_train: {err_train}, Err_test: {err_test}') # 学習 # ランダムなインデックス生成 random_indexes = np.arange(n_train) np.random.shuffle(random_indexes) for j in range(n_batch): # バッチ単位でデータ取得 mb_indexes = random_indexes[j * batch_size : (j+1) * batch_size] x = X_train[mb_indexes, :] t = y_train[mb_indexes, :] # フォワード/バック/学習 forward_propagation(x, True) back_propagation(t) update() # 誤差推移 plt.plot(train_err_x, train_err_y, label='train') plt.plot(test_err_x, test_err_y, label='test') plt.legend() exec()
結果
Epoch: 0 / 1000, Err_train: 1.0967451690864745, Err_test: 1.120339678212259 Epoch: 100 / 1000, Err_train: 0.2802026453736449, Err_test: 0.35979133236270755 Epoch: 200 / 1000, Err_train: 0.17985655919395388, Err_test: 0.23530715133737592 Epoch: 300 / 1000, Err_train: 0.13426607312947325, Err_test: 0.1784395949638583 Epoch: 400 / 1000, Err_train: 0.10930626464205259, Err_test: 0.1450545426264224 Epoch: 500 / 1000, Err_train: 0.09426635243050183, Err_test: 0.12205404811245585 Epoch: 600 / 1000, Err_train: 0.0865758047854498, Err_test: 0.1126515925272934 Epoch: 700 / 1000, Err_train: 0.07964906934536074, Err_test: 0.10376797348333272 Epoch: 800 / 1000, Err_train: 0.07440656440943982, Err_test: 0.09741385116909532 Epoch: 900 / 1000, Err_train: 0.07054625114017309, Err_test: 0.09228238737247033

ドロップアウトを噛ませたことで、1ニューロンあたり 1/2 回しか学習してないだけなのにこうも安定するのか…。
学習の圧がかかってるなら学習回数を増やせばさらに誤差が出るはず!
epoch = 2000 # エポック数2倍! batch_size = 8 interval = 100 n_batch = n_train // batch_size # バッチ/エポック # ニューロン初期化 mid_layer1 = Middle(n_in, n_mid, relu_func, relu_func_dash) mid_layer2 = Middle(n_mid, n_mid, relu_func, relu_func_dash) drop_layer1 = Dropout(0.5) drop_layer2 = Dropout(0.5) outputs = Output(n_mid, n_out, soft_max, soft_max_dash) exec()

ナ ゝ ナ ゝ / 十_" ー;=‐ |! |! cト cト /^、_ノ | 、.__ つ (.__  ̄ ̄ ̄ ̄ ・ ・ ミミ:::;,! u `゙"~´ ヾ彡::l/VvVw、 ,yvヾNヽ ゞヾ ,. ,. ,. 、、ヾゝヽr=ヾ ミ::::;/  ゙̄`ー-.、 u ;,,; j ヾk'! ' l / 'レ ^ヽヘ\ ,r゙ゞ゙-"、ノ / l! !ヽ 、、 | ミ/ J ゙`ー、 " ;, ;;; ,;; ゙ u ヾi ,,./ , ,、ヾヾ | '-- 、..,,ヽ j ! | Nヾ| '" _,,.. -─ゝ.、 ;, " ;; _,,..._ゞイ__//〃 i.! ilヾゞヽ | 、 .r. ヾ-、;;ノ,.:-一'"i j / ,.- 、 ヾヽ、 ;; ;; _,-< //_,,\' "' !| :l ゙i !_,,ヽ.l `ー─-- エィ' (. 7 / : ' ・丿  ̄≠Ξイ´,-、 ヽ /イ´ r. `ー-'メ ,.-´、 i u ヾ``ー' イ \_ _,,......:: ´゙i、 `¨ / i ヽ.__,,... ' u ゙l´.i・j.冫,イ゙l / ``-、..- ノ :u l u  ̄ ̄ 彡" 、ヾ ̄``ミ::.l u j i、`ー' .i / /、._ `'y / u `ヽ ゙:l ,.::- 、,, ,. ノ ゙ u ! /_  ̄ ー/ u / _,,..,,_ ,.ィ、 / | /__ ``- 、_ l l ``ーt、_ / / ゙ u ,./´ " ``- 、_J r'´ u 丿 .l,... `ー一''/ ノ ト 、,,_____ ゙/ / ./__ ー7 /、 l '゙ ヽ/ ,. '" \`ー--- ",.::く、 /;;;''"  ̄ ̄ ───/ ゙ ,::' \ヾニ==='"/ `- 、 ゙ー┬ '´ / \..,,__ 、 .i:⌒`─-、_,.... l / `ー┬一' ヽ :l / , ' `ソヽ ヾヽ l ` `ヽ、 l ./ ヽ l ) ,; / ,' '^i