多層ニューラルネットで過学習させてみる
実際過学習がどの程度影響するのかを検証してみる。
ニューロンのひな型は このへん で作ったものを流用。
import numpy as np wb_width = 0.1 # 重みとバイアスの広がり方 eta = 0.01 # 学習係数 class Neuron: def __init__(self, n_upper, n, activation_function, differential_function): self.w = wb_width * np.random.randn(n_upper, n) # ランダムなのが確立勾配法 self.b = wb_width * np.random.randn(n) self.grad_w = np.zeros((n_upper, n)) self.grad_b = np.zeros((n)) self.activation_function = activation_function self.differential_function = differential_function def update(self): self.w -= eta * self.grad_w self.b -= eta * self.grad_b def forward(self, x): self.x = x u = x.dot(self.w) + self.b self.y = self.activation_function(u) return self.y def backword(self, t): delta = self.differential_function(self.y, t) self.grad_w = self.x.T.dot(delta) self.grad_b = np.sum(delta, axis=0) self.grad_x = delta.dot(self.w.T) return self.grad_x def show(self): print(json.dumps(self.w.tolist())) print(json.dumps(self.b.tolist())) class Output(Neuron): pass class Middle(Neuron): def backword(self, grad_y): delta = self.differential_function(grad_y, self.y) self.grad_w = self.x.T.dot(delta) self.grad_b = delta.sum(axis = 0) self.grad_x = delta.dot(self.w.T) return self.grad_x
活性関数は ReLU で、出力層にはソフトマックス関数を利用。
損失関数には交差エントロピーを使う。(最適化には確率的勾配降下法)
前回は2層(中間層8+出力層3)で過学習らしい話はなかったので、今回はわざと中間層ニューロンを 25 個とかにする。
def relu_func(x): return np.where(x <= 0, 0, x) def relu_func_dash(y, t): return y * np.where(t <= 0, 0, 1) def soft_max(u): return np.exp(u) / np.sum(np.exp(u), axis=1, keepdims = True) def soft_max_dash(y, t): return y - t n_in = 4 n_mid = 25 n_out = 3 mid_layer1 = Middle(n_in, n_mid, relu_func, relu_func_dash) mid_layer2 = Middle(n_mid, n_mid, relu_func, relu_func_dash) outputs = Output(n_mid, n_out, soft_max, soft_max_dash) def forward_propagation(x): return outputs.forward(mid_layer2.forward(mid_layer1.forward(x))) def back_propagation(t): mid_layer1.backword(mid_layer2.backword(outputs.backword(t))) def update(): mid_layer1.update() mid_layer2.update() outputs.update() def get_err(result, t, batch_size): """交差エントロピー誤差""" return -np.sum(t * np.log(result + 1e-7)) / batch_size
データも読み込もうか
from sklearn import datasets iris_data = datasets.load_iris() input_data = iris_data.data correct_data = iris_data.target n_data = len(correct_data)
データを標準化( 式はこの辺から取得 )して
def standardize(x): av = np.average(x, axis=0) std = np.std(x, axis=0) return (x - av) / std input_data = standardize(input_data)
結果も One-Hot 表現に修正
def to_one_hot(v): if v == 0: return [1, 0, 0] elif v == 1: return [0, 1, 0] else: return [0, 0, 1] correct_data = np.array([to_one_hot(v) for v in correct_data])
Iris データを教師データと検証データに分離。
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(input_data, correct_data, random_state=0) # データ数 n_train = X_train.shape[0] n_test = X_test.shape[0] print(f'Training: {n_train} and Tests: {n_test}')
Training: 112 and Tests: 38
まぁこんなもんでしょ。いざ尋常に…一本目…勝負!(ミニバッチで試行)
epoch = 1000 batch_size = 8 interval = 100 n_batch = n_train // batch_size # バッチ/エポック # 誤差記録用 train_err_x = [] train_err_y = [] test_err_x = [] test_err_y = [] def exec(): for i in range(epoch): # 誤差測定 x_res = forward_propagation(X_train) err_train = get_err(x_res, y_train, n_train) y_res = forward_propagation(X_test) err_test = get_err(y_res, y_test, n_test) train_err_x.append(i) train_err_y.append(err_train) test_err_x.append(i) test_err_y.append(err_test) # 途中経過 if i % interval == 0: print(f'Epoch: {i} / {epoch}, Err_train: {err_train}, Err_test: {err_test}') # 学習 # ランダムなインデックス生成 random_indexes = np.arange(n_train) np.random.shuffle(random_indexes) for j in range(n_batch): # バッチ単位でデータ取得 mb_indexes = random_indexes[j * batch_size : (j+1) * batch_size] x = X_train[mb_indexes, :] t = y_train[mb_indexes, :] # フォワード/バック/学習 forward_propagation(x) back_propagation(t) update() exec()
Epoch: 0 / 1000, Err_train: 1.1188678725088852, Err_test: 1.0741287845797183 Epoch: 100 / 1000, Err_train: 0.022156452346814733, Err_test: 0.09437069784152875 Epoch: 200 / 1000, Err_train: 0.009053804027720418, Err_test: 0.18885028835742923 Epoch: 300 / 1000, Err_train: 0.0069379617839766105, Err_test: 0.21728744760885677 Epoch: 400 / 1000, Err_train: 0.0021000353306268823, Err_test: 0.2657830359289565 Epoch: 500 / 1000, Err_train: 0.001363432803194363, Err_test: 0.2931972571973713 Epoch: 600 / 1000, Err_train: 0.0009618036538362834, Err_test: 0.3163168971352748 Epoch: 700 / 1000, Err_train: 0.0007259607208371508, Err_test: 0.32935992577710727 Epoch: 800 / 1000, Err_train: 0.0005821356710873422, Err_test: 0.34061422861356483 Epoch: 900 / 1000, Err_train: 0.00048006676240412764, Err_test: 0.3519300595577461
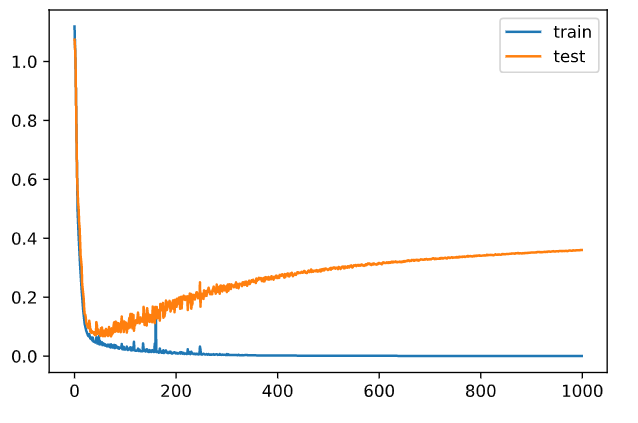
回を重ねるごとに、学習データ「train」への適合が安定化して、代わりに test の誤差が広がっていく。 完全に過学習です。本当にありがとうございましたwww
これ 100 エポ位で安定するんじゃね?ってことでやってみる。
epoch = 101 batch_size = 8 interval = 100 n_batch = n_train // batch_size # バッチ/エポック train_err_x = [] train_err_y = [] test_err_x = [] test_err_y = [] n_in = 4 n_mid = 25 n_out = 3 # 学習をリセット mid_layer1 = Middle(n_in, n_mid, relu_func, relu_func_dash) mid_layer2 = Middle(n_mid, n_mid, relu_func, relu_func_dash) outputs = Output(n_mid, n_out, soft_max, soft_max_dash) # やってみる exec() plt.plot(train_err_x, train_err_y, label='train') plt.plot(test_err_x, test_err_y, label='test') plt.legend()
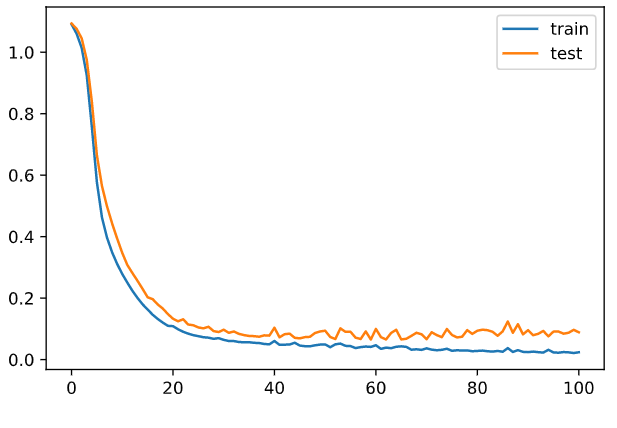
単純にニューロン多すぎだと思うので、8 個まで減らす
epoch = 200 batch_size = 8 interval = 100 n_batch = n_train // batch_size # バッチ/エポック train_err_x = [] train_err_y = [] test_err_x = [] test_err_y = [] n_in = 4 n_mid = 8 # 減らした n_out = 3 mid_layer1 = Middle(n_in, n_mid, relu_func, relu_func_dash) mid_layer2 = Middle(n_mid, n_mid, relu_func, relu_func_dash) outputs = Output(n_mid, n_out, soft_max, soft_max_dash) # やってみる exec() plt.plot(train_err_x, train_err_y, label='train') plt.plot(test_err_x, test_err_y, label='test') plt.legend()
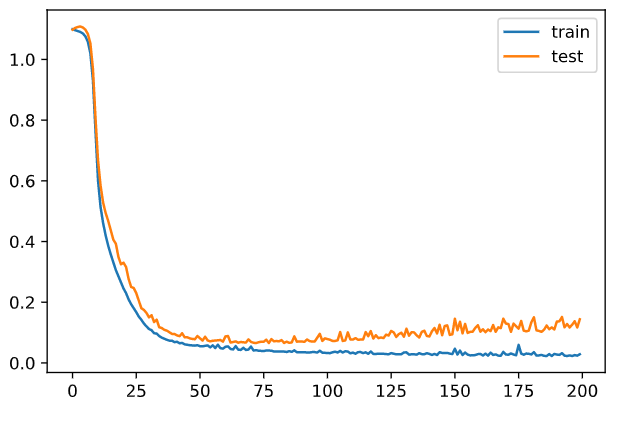
誤差増えてるしwwww
やっぱし学習打ち切りが良いのではなかろうかって雰囲気。